题目内容
讨论当α从0°到180°变化时,曲线x2+y2cosα=1怎样变化?
考点:曲线与方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:分类讨论,结合圆、椭圆、双曲线的方程,即可得出结论.
解答:
解:当α=0°时,cos0°=1,曲线x2+y2=1为一个单位圆;…(2分)
当0°<α<90°时,0<cosα<1,曲线
+
=1为焦点在y轴上的椭圆;…(5分)
当α=90°时,cos90°=0,曲线x2=1为两条平行的垂直于x轴的直线;…(7分)
当90°<α<1800时,-1<cosα<0,曲线
-
=1为焦点在x轴上的双曲线;…(10分)
当α=180°时,cos180°=-1,曲线x2-y2=1为焦点在x轴上的等轴双曲线.…(12分)
当0°<α<90°时,0<cosα<1,曲线
| y2 | ||
|
| x2 |
| 1 |
当α=90°时,cos90°=0,曲线x2=1为两条平行的垂直于x轴的直线;…(7分)
当90°<α<1800时,-1<cosα<0,曲线
| x2 |
| 1 |
| y2 | ||
-
|
当α=180°时,cos180°=-1,曲线x2-y2=1为焦点在x轴上的等轴双曲线.…(12分)
点评:本题考查圆、椭圆、双曲线的方程,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知△ABC中,tanA=-
,那么cosA等于( )
| 5 |
| 12 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
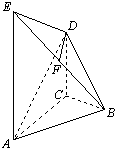 在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.
在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.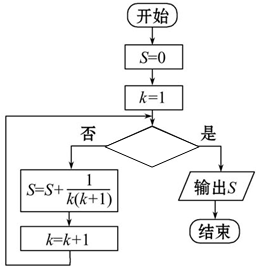 已知算法框图如下:
已知算法框图如下: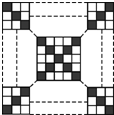 如图所示,在一个(2n-1)×(2n-1)(n∈N且n≥2)的正方形网格内涂色,要求两条对角线的网格涂黑色,其余网格涂白色.若用f(n)表示涂白色网格的个数与涂黑色网格的个数的比值,则f(n)的最小值为
如图所示,在一个(2n-1)×(2n-1)(n∈N且n≥2)的正方形网格内涂色,要求两条对角线的网格涂黑色,其余网格涂白色.若用f(n)表示涂白色网格的个数与涂黑色网格的个数的比值,则f(n)的最小值为