题目内容
解关于x不等式:
(1)ax2-(2a+2)x+4>0(a∈R)
(2)x2+x+m≤0(m∈R)
(1)ax2-(2a+2)x+4>0(a∈R)
(2)x2+x+m≤0(m∈R)
考点:一元二次不等式的应用
专题:计算题,不等式的解法及应用
分析:分类讨论,结合对应方程的根,即可得出结论.
解答:
解:(1)不等式可化为(x-2)(ax-2)>0,
①a=0时,解集为(2,+∞);
②a>1时,解集为(-∞,
)∪(2,+∞);
③a<0时,解集为(
,2);
④0<a<1时,解集为(-∞,2)∪(
,+∞);
⑤a=1时,解集为(-∞,2)∪(2,+∞);
(2)△=1-4m≤0,即m≥
时,解集为R,
m<
时,解集为{x|x=
}.
①a=0时,解集为(2,+∞);
②a>1时,解集为(-∞,
| 2 |
| a |
③a<0时,解集为(
| 2 |
| a |
④0<a<1时,解集为(-∞,2)∪(
| 2 |
| a |
⑤a=1时,解集为(-∞,2)∪(2,+∞);
(2)△=1-4m≤0,即m≥
| 1 |
| 4 |
m<
| 1 |
| 4 |
-1±
| ||
| 2 |
点评:本题考查解关于x不等式,考查学生的计算能力,考查分类讨论的数学思想,正确分类是关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
“k=-1”是“两直线kx+3y-2=0和(2-k)x+y-7=0互相垂直”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
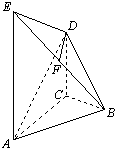 在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.
在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.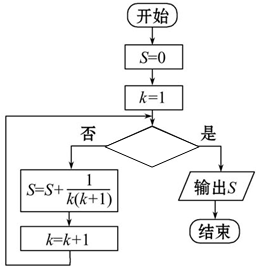 已知算法框图如下:
已知算法框图如下: