题目内容
为改变闽江口环境，加强对化工厂污染源处理，某政协委员针对闽江口环境状况进行了实地调研．据测定，该处的污染指数y与到污染源的距离x成反比，同时与附近污染源的强度m成正比，且比例系数为k，即y=
，若该处与污染源的距离为4km，污染源的强度为2时，则污染指数y等于1．现已知相距36km的A，B两家化工厂（污染源）的污染强度分别为正数a、b，它们连线上任意一点C处的污染指数y等于两化工厂对该处的污染指数之和．设AC=x（km）．（0＜x＜36）
（1）试将y表示为x的函数；
（2）现准备在A，B连线上C处建健身房，若a=1，b=25时，请问C在何处是最佳选择，并说明理由．
| km |
| x |
（1）试将y表示为x的函数；
（2）现准备在A，B连线上C处建健身房，若a=1，b=25时，请问C在何处是最佳选择，并说明理由．
考点：基本不等式在最值问题中的应用,函数解析式的求解及常用方法
专题：应用题,导数的概念及应用
分析：（1）求出点C受A、B污染源污染指数，即可得到点C处污染指数；
（2）求导函数，确定函数的单调性，从而可得函数的极值与最值，进而可得结论．
（2）求导函数，确定函数的单调性，从而可得函数的极值与最值，进而可得结论．
解答：
解：（1）设比例系数为k，由1=
得k=2．
设点C受A污染源污染指数为
，点C受B污染源污染指数为
，
从而点C处污染指数y=
+
（0＜x＜36）；
（2）a=1，b=25时，y=
+
（0＜x＜36）
∴y′=2[-
+
]，
令y′=0，得x=6或x=-9（舍去），
当x∈（0，6）时，函数单调递减；当x∈（6，+∞）时，函数单调递增，
∴x=6是唯一的极小值点，即为函数的最小值点．
| 2k |
| 4 |
设点C受A污染源污染指数为
| 2a |
| x |
| 2b |
| 36-x |
从而点C处污染指数y=
| 2a |
| x |
| 2b |
| 36-x |
（2）a=1，b=25时，y=
| 2 |
| x |
| 50 |
| 36-x |
∴y′=2[-
| 1 |
| x2 |
| 25 |
| (36-x)2 |
令y′=0，得x=6或x=-9（舍去），
当x∈（0，6）时，函数单调递减；当x∈（6，+∞）时，函数单调递增，
∴x=6是唯一的极小值点，即为函数的最小值点．
点评：本题考查函数模型的构建，考查导数知识的运用，考查函数的最值，属于中档题．
练习册系列答案
相关题目
已知角α的终边过点P（x，-3）且cosα=-
，则x的值为（ ）
| ||
| 2 |
A、±3
| ||||
B、3
| ||||
C、-3
| ||||
D、-
|
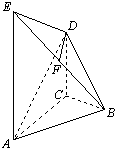在如图所示的几何体中，AE⊥平面ABC，CD∥AE，F是BE的中点，AC=BC=1，∠ACB=90°，AE=2CD=2．
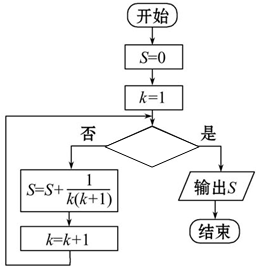已知算法框图如下：