题目内容
17.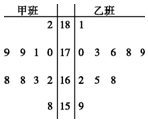 随机 抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示
随机 抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示(1)根据茎叶图判断哪个班的平均身高较高;
(2)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
分析 (1)由题中茎叶图可知:甲班身高集中于160~179cm之间,而乙班身高集中于170~180cm之间,由此能求出结果.
(2)设“身高为176cm的同学被抽中”的事件为A,用(x,y)表示从乙班10名同学中抽中两名身高不低于173cm的同学的身高,由此利用列举法能求出身高为176cm的同学被抽中的概率.
解答 解:(1)由题中茎叶图可知:甲班身高集中于160~179cm之间,
而乙班身高集中于170~180cm之间,因此乙班平均身高高于甲班.
(2)设“身高为176cm的同学被抽中”的事件为A,
用(x,y)表示从乙班10名同学中抽中两名身高不低于173cm的同学的身高,
则所有的基本事件有:
(181,173),(181,176),(181,178),(181,179),(179,173),
(179,176),(179,178),(178,173),(178,176),(176,173),共10个基本事件,
而事件A含有(181,176),(179,176),(178,176),(176,173),共4个基本事件,
故P(A)=$\frac{4}{10}=0.4$.
点评 本题考查茎叶图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
7.已知f(x)=${log}_{2}|x|{+3}^{|x|}$,则f(x2-1)<3的解集为( )
| A. | (-$\sqrt{2}$,-1)∪(-1,0)∪(0,1)∪(1,$\sqrt{2}$) | B. | (-$\sqrt{2}$,0)∪(0,$\sqrt{2}$) | ||
| C. | (-$\sqrt{2}$,$\sqrt{2}$) | D. | (-$\sqrt{2}$,-1)∪(1,$\sqrt{2}$) |
5.要得到函数$y=3sin(x+\frac{π}{2})$的图象,只需将函数y=3sin(2x-$\frac{π}{6}$)的图象上所有点的( )
| A. | 横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),所得图象再向左平移$\frac{2π}{3}$个单位长度. | |
| B. | 横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),所得图象再向右平移$\frac{π}{6}$个单位长度. | |
| C. | 横坐标伸长到原来的2倍(纵坐标不变),所得图象再向左平移$\frac{2π}{3}$个单位长度. | |
| D. | 横坐标伸长到原来的2倍(纵坐标不变),所得图象再向右平移$\frac{π}{6}$个单位长度. |
9.如图所示某公司的组织结构图,信息部被( )直接领导


| A. | 专家办公室 | B. | 开发部 | C. | 总工程师 | D. | 总经理 |
6.在(0,2π)内使sin x>|cos x|的x的取值范围是( )
| A. | ($\frac{π}{4}$,$\frac{3π}{4}$) | B. | ($\frac{π}{4}$,$\frac{π}{2}$]∪($\frac{5π}{4}$,$\frac{3π}{2}$] | C. | ($\frac{π}{4}$,$\frac{π}{2}$) | D. | ($\frac{5π}{4}$,$\frac{7π}{4}$) |
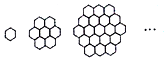 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似的看作是一个正六边形,如图为一组蜂巢的截面图,其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,第六幅图的蜂巢总数为91.
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似的看作是一个正六边形,如图为一组蜂巢的截面图,其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,第六幅图的蜂巢总数为91.