题目内容
5.要得到函数$y=3sin(x+\frac{π}{2})$的图象,只需将函数y=3sin(2x-$\frac{π}{6}$)的图象上所有点的( )| A. | 横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),所得图象再向左平移$\frac{2π}{3}$个单位长度. | |
| B. | 横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),所得图象再向右平移$\frac{π}{6}$个单位长度. | |
| C. | 横坐标伸长到原来的2倍(纵坐标不变),所得图象再向左平移$\frac{2π}{3}$个单位长度. | |
| D. | 横坐标伸长到原来的2倍(纵坐标不变),所得图象再向右平移$\frac{π}{6}$个单位长度. |
分析 直接利用三角函数的图象的伸缩变换和平移变换,求出结果
解答 解:由三角函数的图象的变换的原则可知:将函数y=3sin(2x-$\frac{π}{6}$)图象上的所有点的横坐标变为原来的2倍,纵坐标不变,得到函数y=3sin(x-$\frac{π}{6}$)的图象,然后将函数y=3sin(x-$\frac{π}{6}$)的图象向左平移$\frac{2π}{3}$得到函数y=3sin(x$+\frac{2π}{3}$-$\frac{π}{6}$)即函数$y=3sin(x+\frac{π}{2})$的图象.
故选A.
点评 本题考查三角函数的图象的变换,注意伸缩变换时不变换初相.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0)的图象与直线y=a(0<a<A)的三个相邻交点的横坐标分别是2,4,8,则f(x)的单调递减区间是( )
| A. | [6kπ,6kπ+3](k∈Z) | B. | [6kπ-3,6kπ](k∈Z) | C. | [6k,6k+3](k∈Z) | D. | [6k-3,6k](k∈Z) |
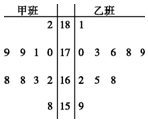 随机 抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示
随机 抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示