题目内容
8.已知sin($\frac{π}{2}$+θ)<0,tan(π-θ)>0,则θ为第 象限角.( )| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
分析 运用三角函数的诱导公式,可得cosθ<0,tanθ<0,由三角函数在各个象限的符号,即可判断θ为第几象限的角.
解答 解:sin($\frac{π}{2}$+θ)<0,可得cosθ<0,
则θ的终边在第二、三象限或x轴的负半轴上;
tan(π-θ)>0,可得-tanθ>0,即tanθ<0,
则θ的终边在第二、四象限.
故θ为第二象限的角.
故选:B.
点评 本题考查三角函数的诱导公式的运用,考查三角函数在各个象限的符号是解题的关键,属于基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
18.某几何体的三视图如图所示,则其体积为( )


| A. | 207 | B. | $216-\frac{9π}{2}$ | C. | 216-36π | D. | 216-18π |
3.某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如表1:
为了研究计算的方便,工作人员将上表的数据进行了处理,t=x-2010,z=y-5得到下表2:
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程$\hat y=\hat bx+\hat a$,其中$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
| 年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
| 储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| z | 0 | 1 | 2 | 3 | 5 |
(Ⅱ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程$\hat y=\hat bx+\hat a$,其中$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
20.已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0)的图象与直线y=a(0<a<A)的三个相邻交点的横坐标分别是2,4,8,则f(x)的单调递减区间是( )
| A. | [6kπ,6kπ+3](k∈Z) | B. | [6kπ-3,6kπ](k∈Z) | C. | [6k,6k+3](k∈Z) | D. | [6k-3,6k](k∈Z) |
18.函数$y=sin(2x-\frac{π}{6})$图象的一条对称轴方程是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{12}$ | D. | $\frac{π}{2}$ |
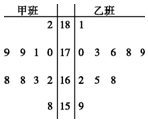 随机 抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示
随机 抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示