题目内容
已知数列{an}中满足a1=15,an+1=an+2n,则
的最小值为( )
| an |
| n |
| A、9 | ||
| B、7 | ||
C、
| ||
D、2
|
考点:数列递推式
专题:等差数列与等比数列
分析:数列{an}中满足a1=15,an+1=an+2n,利用an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=n2-n+15,可得
=
=n+
-1,利用导数考察函数f(x)=x+
(x≥1)的单调性即可得出.
| an |
| n |
| n2-n+15 |
| n |
| 15 |
| n |
| 15 |
| x |
解答:
解:∵数列{an}中满足a1=15,an+1=an+2n,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=2(n-1)+2(n-2)+…+2+15
=
+15
=n2-n+15,
∴
=
=n+
-1,
考察函数f(x)=x+
(x≥1)的单调性,f′(x)=1-
,
由f′(x)>0,解得x>
,此时函数f(x)单调递增;由f′(x)<0,解得1≤x<
,此时函数f(x)单调递减.
∴当n=4时,
的最小值为
=
.
故选:C.
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=2(n-1)+2(n-2)+…+2+15
=
| (n-1)(2+2n-2) |
| 2 |
=n2-n+15,
∴
| an |
| n |
| n2-n+15 |
| n |
| 15 |
| n |
考察函数f(x)=x+
| 15 |
| x |
| 15 |
| x2 |
由f′(x)>0,解得x>
| 15 |
| 15 |
∴当n=4时,
| an |
| n |
| 42-4+15 |
| 4 |
| 27 |
| 4 |
故选:C.
点评:本题考查了等差数列的前n项和公式、“累加求和”、利用导数研究函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
过空间任意一点引三条直线,它们所确定的平面个数是( )
| A、1 | B、2 | C、3 | D、1或3 |
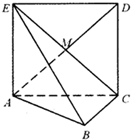 如图,正方形 ACD E所在的平面与平面 A BC垂直,M是C E和 AD的交点,AC⊥BC,且 AC=BC.
如图,正方形 ACD E所在的平面与平面 A BC垂直,M是C E和 AD的交点,AC⊥BC,且 AC=BC. 如图根据下列三视图,想象物体原形,并画出物体的实物草图.
如图根据下列三视图,想象物体原形,并画出物体的实物草图.