题目内容
过空间任意一点引三条直线,它们所确定的平面个数是( )
| A、1 | B、2 | C、3 | D、1或3 |
考点:平面的基本性质及推论
专题:空间位置关系与距离
分析:根据三条直线的位置关系求得平面的个数.
解答:
解:当三条直线在同一个平面内时,它们所确定的平面个数是一个;
当三条直线不在同一个平面内时,它们所确定的平面个数是3个;
故选D.
当三条直线不在同一个平面内时,它们所确定的平面个数是3个;
故选D.
点评:本题考查了直线与平面;注意三条直线是否共面来解答.要全面考虑.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
已知数列{an}中满足a1=15,an+1=an+2n,则
的最小值为( )
| an |
| n |
| A、9 | ||
| B、7 | ||
C、
| ||
D、2
|
若双曲线
-
=1(a>0,b>0)的渐近线与圆(x-2)2+y2=1有公共点,则此双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||||
B、(1,
| ||||
C、(
| ||||
D、[
|
过双曲线
-
=1的右焦点的直线交双曲线的右支于A,B两点,设F是双曲线的左焦点,e是双曲线的离心率,若△ABF为等腰三角形,且∠A=90°,则e2=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、4-2
| ||
B、5-2
| ||
C、6-2
| ||
D、7-2
|
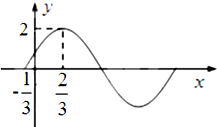 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<