题目内容
已知直线l的参数方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2cosθ.
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设M(-1,
),直线l与圆C相交于点A,B,求|MA||MB|.
|
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设M(-1,
| 3 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(I)由圆C的极坐标方程为ρ=2cosθ,变为ρ2=2ρcosθ,把
代入即可得出;
(II)把直线l的参数方程
(t为参数),代入圆的方程可得t2-3
t+6=0,利用|MA||MB|=t1t2即可得出.
|
(II)把直线l的参数方程
|
| 3 |
解答:
解:(I)由圆C的极坐标方程为ρ=2cosθ,变为ρ2=2ρcosθ,化为x2+y2=2y,配方为x2+(y-1)2=1.
(II)把直线l的参数方程
(t为参数),代入圆的方程可得t2-3
t+6=0,
∴t1t2=6.
∴|MA||MB|=6.
(II)把直线l的参数方程
|
| 3 |
∴t1t2=6.
∴|MA||MB|=6.
点评:本题考查了圆的极坐标方程化为直角坐标方程、直线参数方程的应用,考查了计算能力,属于基础题.

练习册系列答案
相关题目
集合A={1,a,3},B={3,a2,5,6},若A∪B={1,2,3,4,5,6}则a的值为( )
| A、4 | B、±2 | C、2 | D、-2 |
函数f(x)的图象如图所示,则最大、最小值分别为( )
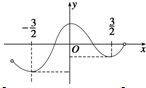

A、f(
| ||||
B、f(0),f(
| ||||
C、f(0),f(-
| ||||
| D、f(0),f(3) |
已知函数y=
+
的单调递减区间是(
,6),则y的最大值是( )
| x-a |
| b-x |
| 5 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列图形中不可能是三棱柱在平面上的投影的是( )
A、 |
B、 |
C、 |
D、 |
某几何体的三视图如图所示,则该几何体的体积为( )


A、
| ||
B、
| ||
| C、16 | ||
| D、32 |
已知数列{an}中满足a1=15,an+1=an+2n,则
的最小值为( )
| an |
| n |
| A、9 | ||
| B、7 | ||
C、
| ||
D、2
|
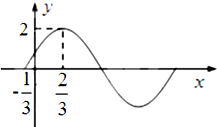 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<