题目内容
已知m2sinα+mcosα-2=0,n2sinα+ncosα-2=0(m,n,α∈R,m≠n),直线l过点P(m,m2),Q(n,n2),则直线l被圆(x-cosα)2+(y-sinα)2=9所截得的弦长为 .
考点:直线与圆的位置关系
专题:直线与圆
分析:由已知条件得到m+n与mn的表达式,再求两点所在的直线方程,表示圆心到直线的距离,与半径比较大小即可.
解答:
解:由题意可得,m、n是方程x2sinα+xcosα-2=0的两个根,∴m+n=-cotα,mn=
.
过(m,m2),(n,n2)两点的直线l方程为:
=
,
即:(m+n)x-y-mn=0,即l:-cotαx-y-
=0,即 cotαx+y-
=0.
∴圆心(cosα,sinα)到直线l的距离
=
=1,
而圆的半径等于3,故弦长为2
=4
,
故答案为:4
.
| -2 |
| sinα |
过(m,m2),(n,n2)两点的直线l方程为:
| y-n2 |
| m2-n2 |
| x-n |
| m-n |
即:(m+n)x-y-mn=0,即l:-cotαx-y-
| -2 |
| sinα |
| 2 |
| sinα |
∴圆心(cosα,sinα)到直线l的距离
|cotα•cosα+sinα-
| ||
|
| |cos2α+sin2α-2| | ||
|
而圆的半径等于3,故弦长为2
| 32-12 |
| 2 |
故答案为:4
| 2 |
点评:本题考察直线与圆的位置关系,间接考察韦达定理和直线方程,注重知识的联系.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
正方体ABCD-A1B1C1D1中,点P为C1D1的中点,则二面角P-AC-D的余弦值是( )


A、
| ||
B、-
| ||
C、
| ||
D、-
|
集合{x|-1<x≤3}用区间表示正确的是( )
| A、(-1,3) |
| B、[-1,3) |
| C、(-1,3] |
| D、[-1,3] |
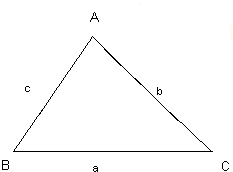 已知锐角△ABC,满足(2a-c)cosB=bcosc,
已知锐角△ABC,满足(2a-c)cosB=bcosc,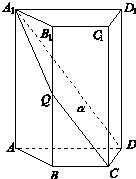 如图,四棱柱ABCD A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC.过A1,C,D三点的平面记为α,BB1与α的交点为Q.
如图,四棱柱ABCD A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC.过A1,C,D三点的平面记为α,BB1与α的交点为Q.