题目内容
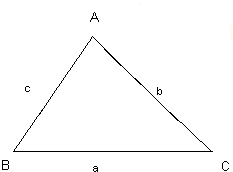已知锐角△ABC，满足（2a-c）cosB=bcosc，求证：（2sinA-sinC）cosB=sinBcosC．
考点：正弦定理,三角函数恒等式的证明
专题：解三角形
分析：直接利用正弦定理，化简已知条件求出结果即可．
解答：
证明：由正弦定理：
=
=
=2R，
∴（2a-c）cosB=bcosc，
化为：（2×2RsinA-2RsinC）cosB=2RsinBcosc，
即：（2sinA-sinC）cosB=sinBcosC．
等式成立．
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
∴（2a-c）cosB=bcosc，
化为：（2×2RsinA-2RsinC）cosB=2RsinBcosc，
即：（2sinA-sinC）cosB=sinBcosC．
等式成立．
点评：本题考查正弦定理的应用，恒等式的证明，基本知识的考查．
练习册系列答案
名校课堂系列答案
相关题目
已知f（x）=loga（8-3ax）在[-1，2]上的减函数，则实数a的取值范围是（ ）
| A、（0，1） | ||
B、(1，
| ||
C、[
| ||
| D、（1，+∞） |
已知全集U={1，2，3，4，5，6，7}，P={1，2，3，4}，Q={3，4，5，6}，（∁UP）∩（∁UQ）=（ ）
| A、{4，7} |
| B、{3，4，5} |
| C、{7} |
| D、{1，2，3，4，5} |
已知集合A={x||x|＜3}，B={x|y=
}，则集合A∩B为（ ）
| x-1 |
| A、[0，3） |
| B、[1，3） |
| C、（1，3） |
| D、（-3，1] |