题目内容
已知数列{an}的前n项和为Sn,Sn=
an-n(n∈N*).
(Ⅰ)求证{an+1}是等比数列,并求数列{an}的通项公式;
(Ⅱ)证明:
+
+
+…
>
-
.
| 3 |
| 2 |
(Ⅰ)求证{an+1}是等比数列,并求数列{an}的通项公式;
(Ⅱ)证明:
| a1 |
| a2 |
| a2 |
| a4 |
| a3 |
| a4 |
| an |
| an+1 |
| n |
| 3 |
| 1 |
| 8 |
考点:等比数列的性质,数列的求和
专题:综合题,等差数列与等比数列
分析:(Ⅰ)依题意可求得a1=2,当n≥2且n∈N*时,有an=Sn-Sn-1,从而得an-3an-1=2,{an+1}是以a1+1=3为首项,3为公比的等比数列,从而可求得an+1=3n,继而可得答案;
(Ⅱ)利用(Ⅰ)的结论an=3n-1,可得
=
=
-
=
-
≥
-
,即可得出结论.
(Ⅱ)利用(Ⅰ)的结论an=3n-1,可得
| an |
| an+1 |
| 3n-1 |
| 3n+1-1 |
| 1 |
| 3 |
| 2 |
| 9•3n-3 |
| 1 |
| 3 |
| 2 |
| 8•3n+3n-3 |
| 1 |
| 3 |
| 2 |
| 8•3n |
解答:
解:(Ⅰ)∵对任意n∈N*,都有Sn=
an-n(n∈N*),且S1=a1,
∴a1=S1=
a1-1,得a1=2…
当n≥2且n∈N*时,有an=Sn-Sn-1=(
an-n)-[
an-1-(n-1)]=
an-
an-1-1,
即an-3an-1=2,
∴an+1=3(an-1+1),由此表明{an+1}是以a1+1=3为首项,3为公比的等比数列.
∴an+1=3•3n-1=3n,
∴an=3n-1
故数列{an}的通项公式为an=3n-1;
(Ⅱ)
=
=
-
=
-
≥
-
,
∴
+
+
+…+
≥
-
(
+
+…+
)=
-
(1-
)>
-
.
| 3 |
| 2 |
∴a1=S1=
| 3 |
| 2 |
当n≥2且n∈N*时,有an=Sn-Sn-1=(
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
即an-3an-1=2,
∴an+1=3(an-1+1),由此表明{an+1}是以a1+1=3为首项,3为公比的等比数列.
∴an+1=3•3n-1=3n,
∴an=3n-1
故数列{an}的通项公式为an=3n-1;
(Ⅱ)
| an |
| an+1 |
| 3n-1 |
| 3n+1-1 |
| 1 |
| 3 |
| 2 |
| 9•3n-3 |
| 1 |
| 3 |
| 2 |
| 8•3n+3n-3 |
| 1 |
| 3 |
| 2 |
| 8•3n |
∴
| a1 |
| a2 |
| a2 |
| a4 |
| a3 |
| a4 |
| an |
| an+1 |
| n |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n |
| n |
| 3 |
| 1 |
| 8 |
| 1 |
| 3n |
| n |
| 3 |
| 1 |
| 8 |
点评:本题考查数列求和,考查等比关系的确定,考查综合分析与运算能力,属于中档题.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
已知函数f(x)的部分图象如图所示,则下列关于f(x)的表达式中正确的是( )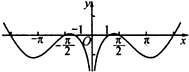

A、f(x)=
| ||
| B、f(x)=(lnx)cos2x | ||
| C、f(x)=(ln|x|)sin2x | ||
| D、f(x)=(ln|x|)cosx |
已知集合A={x|x≥2},B={x|x≤2m2},且A⊆∁RB,那么m的值可以是( )
| A、1 | ||
| B、0 | ||
| C、-1 | ||
D、-
|