题目内容
函数y=
x-cosx,x∈[-
,
]的最大值是 .
| 3 |
| 2 |
| π |
| 2 |
| π |
| 2 |
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:先求导,判断出函数在[-
,
]的单调性,再根据单调性求得最值.
| π |
| 2 |
| π |
| 2 |
解答:
解:∵y=
x-cosx,
∴y'=
+sinx,
∵x∈[-
,
],
∴-1≤sinx≤1,
∴
≤
+sinx≤
,
∴y'>0,
∴原函数在[-
,
]递增,
∴当x=
时,有最大值,y最大为
×
-cos
=
,
故答案为:
| 3 |
| 2 |
∴y'=
| 3 |
| 2 |
∵x∈[-
| π |
| 2 |
| π |
| 2 |
∴-1≤sinx≤1,
∴
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
∴y'>0,
∴原函数在[-
| π |
| 2 |
| π |
| 2 |
∴当x=
| π |
| 2 |
| 3 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 4 |
故答案为:
| 3π |
| 4 |
点评:本题主要考查了导数和函数的最值的关系,关键是判断函数的单调性,属于基础题.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
若有4名学生通过了插班考试,现插入A、B、C三个班中,并且每个班至少插入1人的不同插法有( )
| A、24种 | B、28种 |
| C、36种 | D、32种 |
用秦九韶算法求一元n次多项式f(x)=anxn+an-1xn-1+…+a1x+a0当x=x0时的值时,一个反复执行的步骤是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
已知f1(x)=cosx,f2(x)=f1′(x),f3(x)=f2′(x),f4(x)=f3′(x),…,fn(x)=fn-1′(x),则f2015(x)等于( )
| A、sinx | B、-sinx |
| C、cosx | D、-cosx |
 50个同样大小的立方体木块堆砌成如图所示的形状,现在从前、后、左、右和上面五个方向朝这堆木块喷漆,则有
50个同样大小的立方体木块堆砌成如图所示的形状,现在从前、后、左、右和上面五个方向朝这堆木块喷漆,则有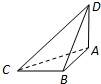 如图,已知球O的球面上四点A,B,C,D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=
如图,已知球O的球面上四点A,B,C,D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=