题目内容

已知直线l：ax+y=1在矩阵A=
2   3
0   1
对应的变换作用下变为直线l′：x+by=1．
（1）求实数a，b的值；
（2）若点P（x0，y0）在直线l上，且A
x0
y0
=
x0
y0
，求点P的坐标．
考点：变换、矩阵的相等
专题：选作题,矩阵和变换
分析：（1）任取直线l：ax+y=1上一点M（x，y），经矩阵A变换后点为M′（x′，y′），利用矩阵乘法得出坐标之间的关系，求出直线l′的方程，从而建立关于a，b的方程，即可求得实数a，b的值；
（2）利用矩阵乘法得出
x0=2x0+3y0
y0=y0
，即可求点P的坐标．
解答： 解：（1）设直线l上一点（x，y）在矩阵A对应的变换下得点（x'，y'），
则
2   3
0   1
x
y
=
x′
y
，
∴
x′=2x+3y
y′=y
代入直线l'，得2x+（b+3）y=1，
∴a=2，b=-2；…（5分）
（2）∵点P（x0，y0）在直线l上，∴2x0+y0=1，
由
2   3
0   1
x0
y0
=
x0
y0
，得
x0=2x0+3y0
y0=y0
，
∴
x0=
3
5
y0=-
1
5
，∴P(
3
5
，-
1
5
)．…（10分）
点评：本题以矩阵为依托，考查矩阵的乘法，关键是正确利用矩阵的乘法公式．
练习册系列答案
相关题目
设集合A={1，3}，B={1，2，4，5}，则A∪B=（　　）
A、{1，2，3，4，5}
B、{2，3，4，5}
C、{1，3}
D、{1}
下列各组数据中方差最大的是（　　）
A、2，6，7
B、2，5，8
C、1，6，8
D、1，5，9
如果a＞b＞0，那么下列不等式成立的是（　　）
A、
1
a
＜
1
b
B、a2＜b2
C、log2a＜log2b
D、（
1
2
）a＞（
1
2
）b
已知向量
a
、
b
满足|
a
|=2，|
b
|=1，且
a
与
b
的夹角为
2π
3
，求：
（1）
a
在
b
的方向上的投影；
（2）（
a
-2
b
）•
b
．
计算：
（1）（C
 
2
100
+C
 
97
100
）÷A
 
3
101
；                      
（2）C
 
3
3
+C
 
3
4
+…+C
 
3
10
．
（3）
C
m
n+1
C
m
n
-
C
n-m+1
n
C
n-m
n
．
已知曲线C的参数方程为
x=
t
-
1
t
y=3(t+
1
t
)+2
（t为参数，t＞0）．求曲线C的普通方程．
在平面直角坐标系xOy中，设圆x2+y2=1在矩阵A=
10
02
对应的变换作用下得到曲线F，求曲线F的方程．
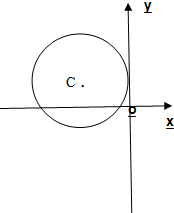如图，已知位于y轴左侧的圆C与y轴相切于点（0，1），且被x轴分成的两段弧长之比为2：1，过点H（0，t）的直线l与圆C相交于M，N两点，且以MN为直径的圆恰好经过坐标原点O．
（1）求圆C的方程；
（2）当t=1时，求出直线l的方程；
（3）求直线OM的斜率k的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网