题目内容
已知命题p:m2-m<0,命题q:
+
=1表示焦点在y轴上的椭圆.
(Ⅰ)若p∧q是真命题,求实数m的取值范围;
(Ⅱ) 若椭圆
+
=1的焦点到双曲线
-
=1的渐近线的距离为
,求m的值.
| y2 |
| 2 |
| x2 |
| 1+4m2 |
(Ⅰ)若p∧q是真命题,求实数m的取值范围;
(Ⅱ) 若椭圆
| y2 |
| 2 |
| x2 |
| 1+4m2 |
| x2 |
| 2 |
| y2 |
| 2 |
| ||
| 2 |
考点:双曲线的简单性质,椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(I)由命题p:m2-m<0,解得0<m<1.命题q:
+
=1表示焦点在y轴上的椭圆,则2>1+4m2>0,解得-
<m<
.由于p∧q是真命题,可得p,q都是真命题.求其交集即可得出.
(2)由双曲线
-
=1可得渐近线y=±x.取y=x.由椭圆
+
=1可得焦点(0,±
).
取(0,
).利用点到直线的距离公式即可得出.
| y2 |
| 2 |
| x2 |
| 1+4m2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由双曲线
| x2 |
| 2 |
| y2 |
| 2 |
| y2 |
| 2 |
| x2 |
| 1+4m2 |
| 1-4m2 |
取(0,
| 1-4m2 |
解答:
解:(I)由命题p:m2-m<0,解得0<m<1.
命题q:
+
=1表示焦点在y轴上的椭圆,则2>1+4m2>0,解得-
<m<
.
∴p∧q是真命题,∴p,q都是真命题.
∴
,解得0<m<
.
∴实数m的取值范围是(0,
).
(II)由双曲线
-
=1可得渐近线y=±x.
取y=x.
由椭圆
+
=1可得焦点(0,±
).
取(0,
).
∵椭圆
+
=1的焦点到双曲线
-
=1的渐近线的距离为
,
∴
=
,
解得m=0.
∴m=0.
命题q:
| y2 |
| 2 |
| x2 |
| 1+4m2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴p∧q是真命题,∴p,q都是真命题.
∴
|
| 1 |
| 2 |
∴实数m的取值范围是(0,
| 1 |
| 2 |
(II)由双曲线
| x2 |
| 2 |
| y2 |
| 2 |
取y=x.
由椭圆
| y2 |
| 2 |
| x2 |
| 1+4m2 |
| 1-4m2 |
取(0,
| 1-4m2 |
∵椭圆
| y2 |
| 2 |
| x2 |
| 1+4m2 |
| x2 |
| 2 |
| y2 |
| 2 |
| ||
| 2 |
∴
|0-
| ||
|
| ||
| 2 |
解得m=0.
∴m=0.
点评:本题考查了复合命题的真假、椭圆与双曲线的标准方程及其性质、点到直线的距离公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
命题p:“?x∈R,2x-1>0”,命题q:“函数f(x)=x-
是奇函数”,则下列命题正确的是( )
| 1 |
| x |
| A、命题“p∧q”是真命题 |
| B、命题“(¬p)∧q”是真命题 |
| C、命题“p∧(¬q)”是真命题 |
| D、命题“(¬p)∧(¬q)”是真命题 |
函数f(x)=ax2+2(a-3)x+1在区间[-3,+∞)上递减,则实数a的取值范围是( )
| A、(-∞,0) | ||
B、[-
| ||
C、[-
| ||
| D、(0,+∞) |
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的体积为( )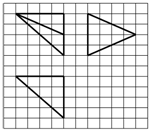

A、
| ||
B、
| ||
C、
| ||
D、
|
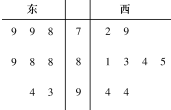 某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.