题目内容

17．已知${C}_{n}^{5}$=${C}_{n}^{6}$，求${C}_{n+3}^{2}$的值．

分析 根据组合数的性质，求出n的值，再代入计算${C}_{n+3}^{2}$的值．

解答 解：∵${C}_{n}^{5}$=${C}_{n}^{6}$，
∴n=5+6=11；
∴${C}_{n+3}^{2}$=${C}_{14}^{2}$=$\frac{14×13}{2×1}$=91．

点评 本题考查了组合数的性质与应用问题，也考查了组合数的计算问题，是基础题目．

练习册系列答案
相关题目
7．已知$\overrightarrow{a}$=（-2，1，3），$\overrightarrow{b}$=（-1，2，1），若$\overrightarrow{a}$⊥（$\overrightarrow{a}$-λ$\overrightarrow{b}$），则实数λ的值为（　　）
A．$\frac{1}{2}$B．2C．-$\frac{1}{2}$D．-2
8．已知函数y=a-bcos（2x+$\frac{π}{6}$）的最大值为3，最小值为-1．
（1）求a，b的值；
（2）设函数g（x）=4asin（bx-$\frac{π}{3}$），求方程g（x）-2=0在区间[$\frac{π}{6}$，$\frac{5}{6}$π]上所有根之和．
5．已知A（1，2），B（3，3），C（7，-1），$\overrightarrow{BM}$=$\frac{1}{4}$$\overrightarrow{BC}$．
（1）求点M的坐标；
（2）证明：$\overrightarrow{OM}$∥$\overrightarrow{AB}$．
12．已知函数f（x）=ax+a-x（a＞0且a≠1）．
（1）判断函数f（x）的奇偶性；
（2）设g（x）=$\frac{1}{f（x）}$，当x∈（0，1）时，求函数g（x）的值域；
（3）若f（1）=$\frac{5}{2}$，设h（x）=a2x+a-2x-2mf（x）的最小值为-7，求实数m的值．
2．圆周上有6个点，任取3个点可以做一个三角形，可得到三角形的个数（　　）
A．6B．12C．18D．20
9．解方程：${C}_{25}^{2x}$=${C}_{25}^{x+4}$．
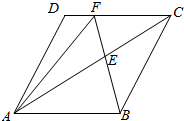6．如图，在菱形ABCD中，AB=1，∠BAD=60°，且E为对角线AC上一点．
（1）求$\overrightarrow{AB}$•$\overrightarrow{AD}$；
（2）若$\overrightarrow{AE}$=2$\overrightarrow{EC}$，求$\overrightarrow{AE}$•$\overrightarrow{AB}$；
（3）连结BE并延长，交CD于点F，连结AF，设$\overrightarrow{CE}$=λ$\overrightarrow{EA}$（0≤λ≤1）．当λ为何值时，可使$\overrightarrow{AF}$•$\overrightarrow{BF}$最小，并求出$\overrightarrow{AF}$$•\overrightarrow{BF}$的最小值．
7．已知函数f（x）=xsinθ+cosθ，其中θ∈[0，2π）．
（Ⅰ）若f（x）在（-∞，+∞）为减函数，求θ的取值范围；
（Ⅱ）若函数f（x）为奇函数，求lnf（sinθ）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网