题目内容
7.已知函数f(x)=xsinθ+cosθ,其中θ∈[0,2π).(Ⅰ)若f(x)在(-∞,+∞)为减函数,求θ的取值范围;
(Ⅱ)若函数f(x)为奇函数,求lnf(sinθ)的值.
分析 (Ⅰ)根据函数的单调性的定义和三角函数图象和性质即可求出;
(2)先根据函数为奇函数,求出θ的值,再求出答案即可.
解答 解:(Ⅰ)设x1,x2∈(-∞,+∞),且x1<x2,
∴f(x1)-f(x2)=x1sinθ+cosθ-x2sinθ-cosθ=(x1-x2)sinθ,
∵f(x)在(-∞,+∞)为减函数,x1<x2,
∴f(x1)-f(x2)>0,
∴(x1-x2)sinθ>0,
∴sinθ<0,
∵θ∈[0,2π),
∴θ∈(π,2π);
(Ⅱ)∵函数f(x)为奇函数,
∴f(-x)=-xsinθ+cosθ=-f(x)=-xsinθ-cosθ,
∴cosθ=0,
∵θ∈[0,2π),
∴θ=$\frac{π}{2}$,或θ=$\frac{3π}{2}$,
∴sinθ=1,或sinθ=-1,
当θ=$\frac{π}{2}$时,f(x)=x,则f(1)=1,则lnf(sinθ)=0,
当θ=$\frac{3π}{2}$时,f(x)=-x,则f(-1)=1,则lnf(sinθ)=0,
综上所述,lnf(sinθ)=0.
点评 本题考查了以三角函数为载体考查了函数的单调性和奇偶性,属于中档题.

练习册系列答案
相关题目
16.已知以直线y=±kx(k>0)为渐近线的双曲线$\frac{{y}^{2}}{{a}^{2}}-\frac{{x}^{2}}{{b}^{2}}=1$(a>0,b>0)的离心率为e,且$\frac{1}{k}$和e是方程${x}^{2}+mx+\sqrt{6}=0$的两个根,则该双曲线的渐近线方程为( )
| A. | $y=±\frac{\sqrt{2}}{2}x$ | B. | $y=±\sqrt{2}x$ | C. | y=±2x | D. | y=$±\frac{1}{2}x$ |
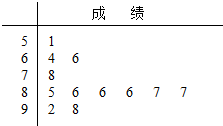 北京时间2015年07月31日17时57分,在马来西亚首都吉隆坡举行的国际奥委会第128次全会上,国际奥委会主席托马斯.巴赫宣布北京赢得2022年第二十四届冬季奥林匹克运动会(以下简称冬奥会)的举办权,华夏大地一片欢腾,某高中为了调查学生对冬奥会的了解惰况,组织了“冬奥会知多少”的知识问卷测试,从该校2400名学生中随机抽取12人进行知识问卷测试,测试成绩(百分制)以茎叶图形式表示(如图所示),根据主办方标准,测试成绩低于80分的为“非体育迷”,不低于80分的为“体育迷”,
北京时间2015年07月31日17时57分,在马来西亚首都吉隆坡举行的国际奥委会第128次全会上,国际奥委会主席托马斯.巴赫宣布北京赢得2022年第二十四届冬季奥林匹克运动会(以下简称冬奥会)的举办权,华夏大地一片欢腾,某高中为了调查学生对冬奥会的了解惰况,组织了“冬奥会知多少”的知识问卷测试,从该校2400名学生中随机抽取12人进行知识问卷测试,测试成绩(百分制)以茎叶图形式表示(如图所示),根据主办方标准,测试成绩低于80分的为“非体育迷”,不低于80分的为“体育迷”,