题目内容
18．设x，y满足约束条件$\left\{\begin{array}{l}{x+y≥1}\\{x-2y≥-2}\\{3x-2y≤3}\end{array}\right.$，则z=x+2y的最大值是7．分析 由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合求得最优解，联立方程组求得最优解的坐标，代入目标函数得答案．
解答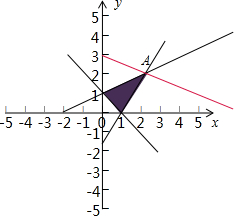 
解：由约束条件$\left\{\begin{array}{l}{x+y≥1}\\{x-2y≥-2}\\{3x-2y≤3}\end{array}\right.$，做出可行域如图，
化目标函数z=x+2y为直线方程的斜截式y=-$\frac{1}{2}$x+$\frac{z}{2}$．
由图可知，当直线y=-$\frac{1}{2}$x+$\frac{z}{2}$过可行域内的点B时，直线在y轴上的截距最大，z最大．
联立$\left\{\begin{array}{l}{x-2y=-2}\\{3x-2y=3}\end{array}\right.$，解得A（$\frac{5}{2}$，$\frac{9}{4}$），
则zmax=$\frac{5}{2}$+2×$\frac{9}{4}$=7．
故答案为：7．
点评 本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
智能训练练测考系列答案
相关题目
14．已知函数$f（x）={sin^4}x+{cos^4}x，x∈[-\frac{π}{4}，\frac{π}{4}]$，若f（x1）＜f（x2），则一定有（ ）
| A． | x1＜x2 | B． | x1＞x2 | C． | ${x_1}^2＜{x_2}^2$ | D． | ${x_1}^2＞{x_2}^2$ |
9．已知正数a，b满足a+b=4，则曲线f（x）=lnx+$\frac{x}{b}$在点（a，f（a））处的切线的倾斜角的取值范围为（ ）
| A． | [$\frac{π}{4}$，+∞） | B． | [$\frac{π}{4}$，$\frac{5π}{12}$） | C． | [$\frac{π}{4}$，$\frac{π}{2}$） | D． | [$\frac{π}{4}$，$\frac{π}{3}$） |
13．函数y=2cos（ωx+ϕ）（ω＞0且|ϕ|＜$\frac{π}{2}$），在区间$[{-\frac{π}{3}，\frac{π}{6}}]$上单调递增，且函数值从-2增大到2，那么此函数图象与y轴交点的纵坐标为（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $\frac{{\sqrt{6}+\sqrt{2}}}{2}$ |
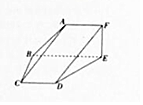如图，平面ABEF⊥平面CBED，四边形ABEF为直角三角形，∠AFE=∠FEB=90°，四边形CBED为等腰梯形，CD∥BE，且BE=2AF=2CD=2BC=2EF=4．