题目内容
3.命题p:“?x∈R,x2-x+1>0”,则?p为?x∈R,x2-x+1≤0.分析 利用全称命题的否定是特称命题写出结果即可.
解答 解:因为全称命题的否定是特称命题,
所以命题p:“?x∈R,x2-x+1>0”,则?p为:?x∈R,x2-x+1≤0.
故答案为:?x∈R,x2-x+1≤0.
点评 本题考查命题的否定,特称命题与全称命题的否定关系,是基础题.

练习册系列答案
相关题目
13.已知矩形ABCD,PA⊥面ABCD,连接AC、BD、PB、PC、PD,则下列各组向量中数量积不为0的是( )
| A. | $\overrightarrow{PC}$和$\overrightarrow{BD}$ | B. | $\overrightarrow{DA}$和$\overrightarrow{PB}$ | C. | $\overrightarrow{PD}$与$\overrightarrow{AB}$ | D. | $\overrightarrow{PC}$与$\overrightarrow{AD}$ |
14.设x∈R,则“x<1”是“x|x|<1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.直线y=-2x+b一定通过( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一、二、四象限 | D. | 第二、三、四象限 |
12.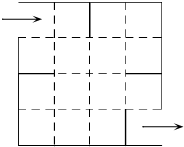 有一种走“方格迷宫”游戏,游戏规则是每次水平或竖直走动一个方格,走过的方格不能重复,只要有一个方格不同即为不同走法.现有如图的方格迷宫,图中的实线不能穿过,则从入口走到出口共有多少种不同走法?( )
有一种走“方格迷宫”游戏,游戏规则是每次水平或竖直走动一个方格,走过的方格不能重复,只要有一个方格不同即为不同走法.现有如图的方格迷宫,图中的实线不能穿过,则从入口走到出口共有多少种不同走法?( )
 有一种走“方格迷宫”游戏,游戏规则是每次水平或竖直走动一个方格,走过的方格不能重复,只要有一个方格不同即为不同走法.现有如图的方格迷宫,图中的实线不能穿过,则从入口走到出口共有多少种不同走法?( )
有一种走“方格迷宫”游戏,游戏规则是每次水平或竖直走动一个方格,走过的方格不能重复,只要有一个方格不同即为不同走法.现有如图的方格迷宫,图中的实线不能穿过,则从入口走到出口共有多少种不同走法?( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
13.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与直线x=$\frac{{a}^{2}}{c}$交于点M,设其右焦点为F,且点F到渐近线的距离为d,则( )
| A. | |MF|>d | B. | |MF|<d | C. | |MF|=d | D. | 与a,b的值有关 |
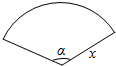 如图,用一根长为10m绳索围成了一个圆心角小于x且半径不超过3m的扇形场地,设扇形的半径为xm,面积为Scm2.
如图,用一根长为10m绳索围成了一个圆心角小于x且半径不超过3m的扇形场地,设扇形的半径为xm,面积为Scm2.