题目内容
在△ABC中，已知
=
，则△ABC的形状为 ．
| cosA |
| cosB |
| a |
| b |
考点：余弦定理
专题：计算题,解三角形
分析：利用正弦定理化边为角，然后由差角正弦公式可化简，进而可得答案．
解答：
解：由正弦定理，得
=
即为
=
，
∴cosAsinB=sinAcosB，
∴sin（A-B）=0，则A-B=0，即A=B，
∴△ABC为等腰三角形，
故答案为：等腰三角形．
| cosA |
| cosB |
| a |
| b |
| cosA |
| cosB |
| sinA |
| sinB |
∴cosAsinB=sinAcosB，
∴sin（A-B）=0，则A-B=0，即A=B，
∴△ABC为等腰三角形，
故答案为：等腰三角形．
点评：该题考查正弦定理、两角差的正弦函数，属基础题．
练习册系列答案
相关题目
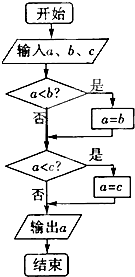阅读如图的算法流程图：若a=sin60°，b=cos60°，c=tan60°，则输出的应该是