题目内容
15．从某企业生产的某种产品中随机抽取10件，测量这些产品的一项质量指标，其频率分布表如下：| 质量指标值分组 | [10，30） | [30，50） | [50，70] |
| 频率 | 0.1 | 0.6 | 0.3 |
| A． | 140 | B． | 142 | C． | 143 | D． | 134.8 |
分析 根据定义，计算质量指标的样本平均数$\overline{x}$和方差S2．
解答 解：根据题意，计算质量指标的样本平均数为：
$\overline{x}$=20×0.1+40×0.6+60×0.3=44；
所以质量指标的样本方差为
S2=（44-20）2×0.1+（44-40）2×0.6+（44-60）2×0.3=134.8．
故选：D．
点评 本题考查了频率分布表、平均数和方差的计算问题，是基础题．
练习册系列答案
相关题目
20．
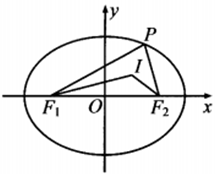设P为椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上的动点，F1、F2为椭圆C的焦点，I为△PF1F2的内心，则直线IF1和直线IF2的斜率之积（ ）
设P为椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上的动点，F1、F2为椭圆C的焦点，I为△PF1F2的内心，则直线IF1和直线IF2的斜率之积（ ）| A． | 是定值 | B． | 非定值，但存在最大值 | ||
| C． | 非定值，但存在最小值 | D． | 非定值，且不存在最值 |
7．$\overrightarrow{AB}$+$\overrightarrow{AC}$-$\overrightarrow{BC}$+$\overrightarrow{BA}$ 化简后等于（ ）
| A． | 3$\overrightarrow{AB}$ | B． | $\overrightarrow{BA}$ | C． | $\overrightarrow{AB}$ | D． | $\overrightarrow{CA}$ |