题目内容
已知函数f(x)=
,则下列结论中正确的是( )
| sin(x+π) |
| cos(π-x) |
| A、f(x)的最小正周期是2π | ||
| B、f(x)在[4,5]上单调递增 | ||
C、f(x)的图象关于x=
| ||
D、f(x)的图象关于点(
|
考点:运用诱导公式化简求值,同角三角函数基本关系的运用
专题:三角函数的求值
分析:f(x)解析式利用诱导公式化简后,再利用同角三角函数间基本关系变形,求出最小正周期,利用正切函数的对称性及增减性判断即可.
解答:
解:f(x)=
=tanx,
∵ω=1,∴T=
=π,即最小正周期为π,选项A错误;
正切函数y=tanx的递增区间为-
+kπ<x<
+kπ,k∈Z,
而4<x=
<5时,f(x)没有意义,选项B错误;
f(x)图象关于(
,0),k∈Z对称,选项C错误;
f(x)的图象关于点(
,0)对称,选项D正确,
故选D
| -sinx |
| -cosx |
∵ω=1,∴T=
| π |
| 1 |
正切函数y=tanx的递增区间为-
| π |
| 2 |
| π |
| 2 |
而4<x=
| 3π |
| 2 |
f(x)图象关于(
| π |
| 2 |
f(x)的图象关于点(
| 3π |
| 2 |
故选D
点评:此题考查了运用诱导公式化简求值,以及同角三角函数间基本关系的运用,熟练掌握诱导公式是解本题的关键.

练习册系列答案
相关题目
函数y=2+
sinx的最小正周期和最小值分别为( )
| 2 |
| A、π,1 | ||
| B、2π,1 | ||
C、π,2-
| ||
D、2π,2-
|
定积分
(-3)dx等于( )
| ∫ | 3 1 |
| A、-6 | B、6 | C、-3 | D、3 |
已知i是虚数单位,若(2-i)•z=-i,则z=( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
 一观览车的主架示意图如图所示,其中O为轮轴的中心,距地面32m(即OM长),巨轮的半径为30m,AM=BP=2m,巨轮逆时针旋转且每12分钟转动一圈.若点M为吊舱P的初始位置,经过t分钟,该吊舱P距离地面的高度为h(t)m,则h(t)=( )
一观览车的主架示意图如图所示,其中O为轮轴的中心,距地面32m(即OM长),巨轮的半径为30m,AM=BP=2m,巨轮逆时针旋转且每12分钟转动一圈.若点M为吊舱P的初始位置,经过t分钟,该吊舱P距离地面的高度为h(t)m,则h(t)=( )A、30sin(
| ||||
B、30sin(
| ||||
C、30sin(
| ||||
D、30sin(
|
某工厂分别生产甲、乙两种产品1箱时所需要的煤、电以及获得的纯利润如下表所示.
若生产甲、乙两种产品可使用的煤不超过120吨,电不超过60千度,则可获得的最大纯利润和是( )
| 煤(吨) | 电(千度) | 纯利润(万元) | |
| 1箱甲产品 | 3 | 1 | 2 |
| 1箱乙产品 | 1 | 1 | 1 |
| A、60万元 | B、80万元 |
| C、90万元 | D、100万元 |
已知角α的终边与单位圆交于点P(m,n),且n=2m(m≠0)那么sin2α的值是( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
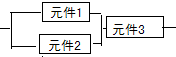 某一部件由三个电子元件按如图所示方式连接而成,元件1或元件2正常工作,则部件正常工作:设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,σ2),若每个元件使用寿命超过1200小时的概率为
某一部件由三个电子元件按如图所示方式连接而成,元件1或元件2正常工作,则部件正常工作:设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,σ2),若每个元件使用寿命超过1200小时的概率为