题目内容
如图，一个几何体的三视图如图所示，则该多面体的几条棱中，最长的棱的长度为（ ）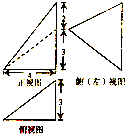
A、3
| ||
B、
| ||
C、
| ||
D、3
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：根据几何体的三视图，得出该几何体是三棱锥，画出它的直观图，求出各条棱长即可．
解答：
解：根据几何体的三视图，得；
该几何体是三棱锥P-ABC，如图所示；
PA=4，AB=3+2=5，C到AB中点D的距离为CD=3，
∴PB=
=
=
，
AC=
=
=
，
BC=
=
，
PC=
=
=
，
∴PB最长，长度为
．
故选：C．
解：根据几何体的三视图，得；该几何体是三棱锥P-ABC，如图所示；
PA=4，AB=3+2=5，C到AB中点D的距离为CD=3，
∴PB=
| PA2+AB2 |
| 42+52 |
| 41 |
AC=
| AD2+CD2 |
| 32+32 |
| 18 |
BC=
| BD2+CD2 |
| 22+32 |
| 13 |
PC=
| PA2+AC2 |
42+(
|
| 34 |
∴PB最长，长度为
| 41 |
故选：C．
点评：本题考查了空间几何体的三视图的应用问题，解题的关键是由三视图得出几何体的结构特征是什么．
练习册系列答案
应用题作业本系列答案
相关题目
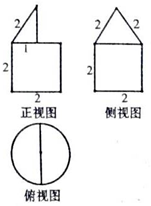
某几何体的三视图如图所示，则该几何体的体积是（ ）
A、（
| ||||
B、（
| ||||
C、（
| ||||
D、（
|
某几何体的正视图和俯视图如图所示，若正视图是面积为3的矩形，俯视图是边长为1的正三角形，则该几何体的侧视图的面积为（ ）A、
| ||||
B、3
| ||||
| C、3 | ||||
| D、9 |