题目内容
已知f(x)=(1+x)lnx,g(x)=a(1-x)
(1)是否存在实数a,使g(x)是f(x)在x=1处的切线?
(2)若函数y=f(x)+g(x)是增函数,求实数a的范围.
(1)是否存在实数a,使g(x)是f(x)在x=1处的切线?
(2)若函数y=f(x)+g(x)是增函数,求实数a的范围.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:导数的概念及应用,导数的综合应用,不等式的解法及应用
分析:(1)求出f(x)的导数,求得f(x)在x=1处的切线斜率,切点坐标,即有a=-2,检验即可得到存在;
(2)求出函数y的导数,由函数y=f(x)+g(x)是增函数,即有lnx+
-a≥0在x>0恒成立,运用参数分离和求出右边函数的最大值,即可得到a的范围.
(2)求出函数y的导数,由函数y=f(x)+g(x)是增函数,即有lnx+
| 1+x |
| x |
解答:
解:(1)f(x)=(1+x)lnx的导数为f′(x)=lnx+
,
f(x)在x=1处的切线斜率为k=f′(1)=ln1+2=2,
切点为(1,0),即有a=-2,
即g(x)=-2(1-x)成立,
故存在a为2,使g(x)是f(x)在x=1处的切线;
(2)函数y=f(x)+g(x)=(1+x)lnx+a(1-x)
的导数为y′=lnx+
-a,
由函数y=f(x)+g(x)是增函数,
即有lnx+
-a≥0在x>0恒成立,
即有a-1≤lnx+
,
令h(x)=lnx+
,h′(x)=
-
=
,
当x>1时,h′(x)>0,h(x)递增,
当0<x<1时,h′(x)<0,h(x)递减.
即有h(x)在x=1处取得极小值,也为最小值,且为1.
则有a-1≤1,
即有a≤2.
故a的取值范围是(-∞,2].
| 1+x |
| x |
f(x)在x=1处的切线斜率为k=f′(1)=ln1+2=2,
切点为(1,0),即有a=-2,
即g(x)=-2(1-x)成立,
故存在a为2,使g(x)是f(x)在x=1处的切线;
(2)函数y=f(x)+g(x)=(1+x)lnx+a(1-x)
的导数为y′=lnx+
| 1+x |
| x |
由函数y=f(x)+g(x)是增函数,
即有lnx+
| 1+x |
| x |
即有a-1≤lnx+
| 1 |
| x |
令h(x)=lnx+
| 1 |
| x |
| 1 |
| x |
| 1 |
| x2 |
| x-1 |
| x2 |
当x>1时,h′(x)>0,h(x)递增,
当0<x<1时,h′(x)<0,h(x)递减.
即有h(x)在x=1处取得极小值,也为最小值,且为1.
则有a-1≤1,
即有a≤2.
故a的取值范围是(-∞,2].
点评:本题考查导数的运用:求切线方程和求单调区间、极值和最值,运用导数的几何意义和不等式恒成立思想转化为求函数的最值是解题的关键.

练习册系列答案
相关题目
已知cos(α+
)-sinα=
,则sin(α-
)的值是( )
| π |
| 6 |
| 4 |
| 5 |
| 3 |
| π |
| 6 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
某几何体的三视图如图所示,则该几何体的体积是( )
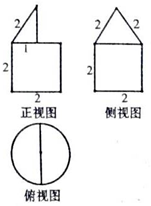

A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|