题目内容
函数y=
的定义域为R，则实数k的取值范围为（ ）
| x |
| kx2+kx+1 |
| A、k＜0或k＞4 |
| B、k≥4或k≤0 |
| C、0≤k＜4 |
| D、0＜k＜4 |
考点：函数的定义域及其求法
专题：计算题,分类讨论,函数的性质及应用
分析：y=
的定义域要使给出的分式函数定义域为实数集，是指对任意实数x分式的分母恒不等于0，对分母的二次三项式进行分类讨论，分k=0，和k≠0讨论，当k≠0时，需要二次三项式对应的二次方程的判别式小于0．
| x |
| kx2+kx+1 |
解答：
解∵函数y=
的定义域为R，
∴kx2+kx+1对?x∈R恒不为零，
当k=0时，kx2+kx+1=1≠0成立；
当k≠0时，需△=k2-4k＜0，解得0＜k＜4．
综上，使函数的定义域为R的实数k的取值范围为[0，4）．
故选：C．
| x |
| kx2+kx+1 |
∴kx2+kx+1对?x∈R恒不为零，
当k=0时，kx2+kx+1=1≠0成立；
当k≠0时，需△=k2-4k＜0，解得0＜k＜4．
综上，使函数的定义域为R的实数k的取值范围为[0，4）．
故选：C．
点评：本题是在知道函数的定义域的前提下求解参数的范围问题，考查了数学转化思想和分类讨论思想，解答此题时容易忽视k=0的情况导致解题出错，此题是基础题．
练习册系列答案
相关题目
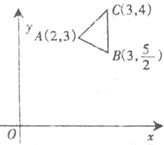已知点（x，y）在△ABC所包围的区域内（包含边界），若B（3，| 5 |
| 2 |
A、a≥-
| ||
| B、a＞0 | ||
C、a≤-
| ||
D、-
|
甲、乙、丙、丁四位同学站成一排照相留念，则甲、乙相邻的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
△ABC顶点A（2，3），B（0，0），C（4，0），则“方程x=2”是“BC边上中线方程”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |