题目内容
将演绎推理：“正弦函数是奇函数，f（x）=sinx2+1是正弦函数，所以f（x）=sinx2+1是奇函数．”以上推理（ ）
| A、结论错误 | B、大前提错误 |
| C、小前提错误 | D、都不正确 |
考点：进行简单的合情推理
专题：探究型,推理和证明
分析：根据三段论的要求：找出大前提，小前提，结论，再判断正误即可．
解答：
解：大前提：正弦函数是奇函数，正确；
小前提：f（x）=sinx2+1正弦函数，因为该函数为复合函数，故错误；
结论：f（x）=sinx2+1是奇函数，因为该函数为偶函数，故错误．
故选C．
小前提：f（x）=sinx2+1正弦函数，因为该函数为复合函数，故错误；
结论：f（x）=sinx2+1是奇函数，因为该函数为偶函数，故错误．
故选C．
点评：本题考查演绎推理的基本方法，属基础题．
练习册系列答案
相关题目
某单位有200名职工，现从中抽取40名职工作样本，用系统抽样的方法，将全体职工随机按1～200编号，并按编号顺序平均分为40组（1-5号，6-10号，…196-200号），若第5组抽出的是23号，则第8组抽到的号码为（ ）
| A、36 | B、39 | C、37 | D、38 |
空间两两相交的三条直线，可以确定的平面个数是（ ）
| A、1 | B、2 | C、1或3 | D、3 |
已知抛物线x2=4y上一点A的纵坐标为3，则点A与抛物线焦点的距离为（ ）
| A、1 | B、2 | C、3 | D、4 |
某地气象台预报“本市明天有雨的概率是95%”．以下理解正确的是（ ）
| A、本市明天将有95%的地区有雨 |
| B、本市明天将有95%的时间有雨 |
| C、明天出行不带雨具肯定会淋雨 |
| D、明天出行不带雨具淋雨的可能性较大 |
已知不同直线m，n和不同平面α，β，给出下列命题：
①若α∥β，m?α，则m∥β；
②若m∥n，n⊥β，m?α，则α⊥β；
③若α∥m，β∥m，则α∥β；
④若α⊥β，m∥α，则m⊥β．
其中的真命题有（ ）
①若α∥β，m?α，则m∥β；
②若m∥n，n⊥β，m?α，则α⊥β；
③若α∥m，β∥m，则α∥β；
④若α⊥β，m∥α，则m⊥β．
其中的真命题有（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
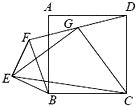如图，四边形ABCD是正方形，△BEF是等腰直角三角形，∠BEF=90°，BE=EF．连接DF，G为DF的重点，连接EG，CG，EC，求证：|