题目内容
已知椭圆C:
+
=1(a>b>0)的焦距是2,离心率是0.5;
(1)求椭圆的方程;
(2)求证:过点A(1,2)倾斜角为45°的直线l与椭圆C有两个不同的交点;又记这两个交点为P、Q,试求出线段PQ的中点M的坐标.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆的方程;
(2)求证:过点A(1,2)倾斜角为45°的直线l与椭圆C有两个不同的交点;又记这两个交点为P、Q,试求出线段PQ的中点M的坐标.
考点:椭圆的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)直接根据焦距是2,离心率是0.5;求出c=1,a=2,再根据a,b,c之间的关系求出b;即可求椭圆的方程;
(2)把直线方程和椭圆方程联立,转化为关于x的一元二次方程,只要对应的判别式大于0即可说明结论.
(2)把直线方程和椭圆方程联立,转化为关于x的一元二次方程,只要对应的判别式大于0即可说明结论.
解答:
(1)解:由题意2c=2,∴c=1,…(2分)
由离心率是0.5,得a=2,∴b=
.…(4分)
∴椭圆的方程为
+
=1. …(6分)
(2)证明:直线l:y-2=tan45°(x-1),即y=x+1.…(8分)
代入
+
=1,整理得:7x2+8x-8=0.…(10分)
∵△=82-4×7×(-8)=288>0…(11分)
∴过点A(1,2)倾斜角为45°的直线l与椭圆有两个不同的交点.
线段PQ的中点M的横坐标为-
,纵坐标为
,即M(-
,
).…(14分)
由离心率是0.5,得a=2,∴b=
| 3 |
∴椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)证明:直线l:y-2=tan45°(x-1),即y=x+1.…(8分)
代入
| x2 |
| 4 |
| y2 |
| 3 |
∵△=82-4×7×(-8)=288>0…(11分)
∴过点A(1,2)倾斜角为45°的直线l与椭圆有两个不同的交点.
线段PQ的中点M的横坐标为-
| 4 |
| 7 |
| 3 |
| 7 |
| 4 |
| 7 |
| 3 |
| 7 |
点评:本题综合考查椭圆的性质及应用和直线与椭圆的位置关系,属于中档题目,解题时要注意性质的灵活运用.

练习册系列答案
相关题目

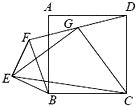 如图,四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF.连接DF,G为DF的重点,连接EG,CG,EC,求证:|
如图,四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF.连接DF,G为DF的重点,连接EG,CG,EC,求证:|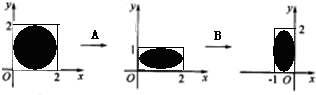 二阶矩阵A,B对应的变换对圆的区域作用结果如图所示.
二阶矩阵A,B对应的变换对圆的区域作用结果如图所示.