题目内容
椭圆C1:
+
=1(a>b>0)过点P(1,
),离心率e=
,A为椭圆C1上一点,B为抛物线y2=
x上一点,且A为线段OB的中点.
(1)求椭圆C1的方程;
(2)求直线AB的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
(1)求椭圆C1的方程;
(2)求直线AB的方程.
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)据题意得:
又a2=b2+c2,解出a,b即可得到椭圆方程;
(2)设A点坐标为(x0,y0),则B点坐标为(2x0,2y0),分别代入椭圆和抛物线方程,解出A点坐标,即可得到AB方程.
|
(2)设A点坐标为(x0,y0),则B点坐标为(2x0,2y0),分别代入椭圆和抛物线方程,解出A点坐标,即可得到AB方程.
解答:
解:(1)据题意得:
又a2=b2+c2,
解得
,
所以椭圆方程为
+
=1.
(2)设A点坐标为(x0,y0),则B点坐标为(2x0,2y0),
分别代入椭圆和抛物线方程得
,
消去y0并整理得:3x02+
x0-12=0,
所以x0=
或x0=-
.
当x0=
时,y0=±
;
当x0=-
时,y0无解.
所以直线AB的方程为y=±
x.
|
解得
|
所以椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设A点坐标为(x0,y0),则B点坐标为(2x0,2y0),
分别代入椭圆和抛物线方程得
|
消去y0并整理得:3x02+
| 3 |
所以x0=
| 3 |
4
| ||
| 3 |
当x0=
| 3 |
| ||
| 2 |
当x0=-
4
| ||
| 3 |
所以直线AB的方程为y=±
| 1 |
| 2 |
点评:本题考查椭圆的方程和性质及运用,考查抛物线方程的运用,考查直线方程的求法,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知焦点在x轴上的椭圆离心率e=
,它的半长轴长等于圆x2+y2-2x-3=0的半径,则椭圆的标准方程是( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知数列{an}满足an=1+
+
+…+
,则ak+1-ak共有( )项.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n2 |
| A、1 | B、k | C、2k | D、2k+1 |
50名学生参加跳远和铅球两项测试,跳远、铅球测试及格的分别有40人和31人,两项测试均不及格的有4人,两项测试全都及格的人数是( )
| A、35 | B、25 | C、28 | D、15 |
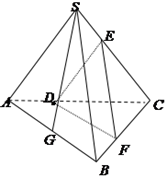 如图,在三棱锥S-ABC中,D、E、F分别是棱AC、BC、SC上的点,且CD=2DA,CE=2ES,CF=2FB,G是AB的中点.求证:SG∥平面DEF.
如图,在三棱锥S-ABC中,D、E、F分别是棱AC、BC、SC上的点,且CD=2DA,CE=2ES,CF=2FB,G是AB的中点.求证:SG∥平面DEF.