题目内容
设函数f(x)=|x-a|+3x,其中a>0,若不等式f(x)≤0的解集为{x|x≤-1},则a的值为 .
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:由题意可得|x-a|≤-3x 的解集为{x|x≤-1}.而由|x-a|≤-3x,求得x≤-
,可得-
=-1,由此求得a的值.
| a |
| 2 |
| a |
| 2 |
解答:
解:由题意可得|x-a|≤-3x 的解集为{x|x≤-1}.
而由|x-a|≤-3x,可得 3x≤x-a≤-3x,求得x≤-
,
∴-
=-1,∴a=2,
故答案为:2.
而由|x-a|≤-3x,可得 3x≤x-a≤-3x,求得x≤-
| a |
| 2 |
∴-
| a |
| 2 |
故答案为:2.
点评:本题主要考查绝对值不等式的解法,体现了等价转化的数学思想,属于基础题.

练习册系列答案
相关题目
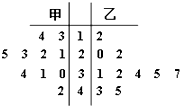 从甲、乙两个城市分别随机抽取10台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示).设甲、乙两组数据的平均数分别为
从甲、乙两个城市分别随机抽取10台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示).设甲、乙两组数据的平均数分别为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若a>b>0则下列不等式不成立的是( )
A、
| ||||
| B、|a|>|b| | ||||
C、log
| ||||
D、a+b<2
|