题目内容
设f（x）=log2x，则f（410）= ．
考点：对数的运算性质
专题：函数的性质及应用
分析：利用对数的运算性质求解．
解答：
解：∵f（x）=log2x，
∴f（410）=log2(410)
=log2(220)
=20．
故答案为：20．
∴f（410）=log2(410)
=log2(220)
=20．
故答案为：20．
点评：本题考查函数值的求法，是基础题，解题时要认真审题，注意对数的运算性质的合理运用．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
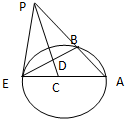如图，过点P作圆O的割线PBA与切线PE，E为切点，连接AE，BE，∠APE的平分线分别与AE、BE相交于C、D，若∠AEB=40°，则∠PCE等于
已知x，y，z均为正数，且x+y+z=2，则
+
+
的最大值是（ ）
| x |
| 2y |
| 3z |
| A、2 | ||
B、2
| ||
C、2
| ||
| D、?3 |