题目内容
四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,则这个五面体的五个面中两两互相垂直的共有 对.
考点:平面与平面垂直的判定,棱锥的结构特征
专题:证明题,空间位置关系与距离
分析:因为PA⊥平面ABCD,得到2组互相垂直的平面.再利用四边形ABCD为正方形得到其他互相垂直的平面即可.
解答:
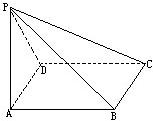 解:因为PA⊥平面ABCD,所以平面PDA⊥平面ABCD,平面PAB⊥平面ABCD,
解:因为PA⊥平面ABCD,所以平面PDA⊥平面ABCD,平面PAB⊥平面ABCD,
又因为四边形ABCD为正方形,所以AB⊥平面PAD⇒平面ABP⊥平面PAD,
同理可得平面PBC⊥平面PAB.平面PAD⊥平面PAB.
故图中互相垂直的平面共有5组.
故答案为:5.
 解:因为PA⊥平面ABCD,所以平面PDA⊥平面ABCD,平面PAB⊥平面ABCD,
解:因为PA⊥平面ABCD,所以平面PDA⊥平面ABCD,平面PAB⊥平面ABCD,又因为四边形ABCD为正方形,所以AB⊥平面PAD⇒平面ABP⊥平面PAD,
同理可得平面PBC⊥平面PAB.平面PAD⊥平面PAB.
故图中互相垂直的平面共有5组.
故答案为:5.
点评:本题考查面面垂直的判定.在证明面面垂直时,其常用方法是在其中一个平面内找两条相交直线和另一平面内的某一条直线垂直.

练习册系列答案
相关题目
函数y=
的定义域为( )
| 1 | |||
|
| A、{x|x≠0} |
| B、{x|x>0} |
| C、{x|x≥0} |
| D、{x|x∈R} |
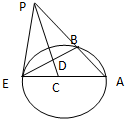 如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线分别与AE、BE相交于C、D,若∠AEB=40°,则∠PCE等于
如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线分别与AE、BE相交于C、D,若∠AEB=40°,则∠PCE等于
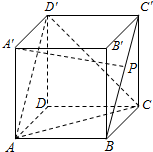 如图,点P在正方体ABCD-A′B′C′D′的面对角线BC′上运动.给出下列三个命题:
如图,点P在正方体ABCD-A′B′C′D′的面对角线BC′上运动.给出下列三个命题: 如图,M是抛物线y2=4x上一点,F是抛物线的焦点,若∠MFO=120°,则MF=
如图,M是抛物线y2=4x上一点,F是抛物线的焦点,若∠MFO=120°,则MF=