题目内容
已知x∈[0,
],求函数y=cosx+sin2x+
的最值.
| π |
| 4 |
| 1 |
| 2 |
考点:三角函数的最值
专题:三角函数的图像与性质
分析:利用三角函数的基本关系式化简函数的表达式为cosx的二次函数,利用换元法求出函数的值域.
解答:
解:由题意y=cosx+sin2x+
=-cos2x+cosx+
=-(cosx-
)2+
,x∈[0,
],…2′
令t=cosx,t∈[
,1]…4′
则y=-(t-
)2+
. …6′
∴当t=
时,ymax=1+
; …8′
当t=1时,ymin=
. …10′
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 7 |
| 4 |
| π |
| 4 |
令t=cosx,t∈[
| ||
| 2 |
则y=-(t-
| 1 |
| 2 |
| 7 |
| 4 |
∴当t=
| π |
| 2 |
| ||
| 2 |
当t=1时,ymin=
| 3 |
| 2 |
点评:本题考查三角函数的化简求值,二次函数闭区间上的最值的求法,考查计算能力.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
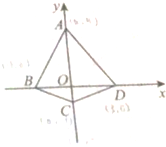 在平面直角坐标系xOy中,四边形ABCD的位置如图所示,A(0,4),B(-2,0),C(0,-1),D(3,0),动点P(x,y)在第一象限,且满足S△PAD=S△PBC,求点P的横、纵坐标满足的关系式(用x表示y),并写出x的取值范围.
在平面直角坐标系xOy中,四边形ABCD的位置如图所示,A(0,4),B(-2,0),C(0,-1),D(3,0),动点P(x,y)在第一象限,且满足S△PAD=S△PBC,求点P的横、纵坐标满足的关系式(用x表示y),并写出x的取值范围.