题目内容
函数y=
的定义域为 .
| log2(2x2-x) |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据函数f(x)的解析式,列出使解析式有意义的不等式组,从而求出f(x)的定义域.
解答:
解:要使函数有意义,x需满足:
,
可得 x≤-
,或x≥1,
故答案为:{ {x|x≤-
,或x≥1},
|
可得 x≤-
| 1 |
| 2 |
故答案为:{ {x|x≤-
| 1 |
| 2 |
点评:本题考查函数定义域的求解,属基础题,要求:开偶次方根被开方数要大于等于零;对数的真数大于零.注意定义域的表示形式.

练习册系列答案
相关题目
已知向量
=(2,x-1),
=(1,-y),其中xy>0,且
∥
,则
的最小值为( )
| AB |
| CD |
| AB |
| CD |
| 8x+y |
| xy |
| A、34 | B、25 | C、27 | D、16 |
阅读如图所示的程序框图,运行相应的程序,输出s的值为( )


| A、62 | B、126 |
| C、254 | D、510 |
设等差数列{an}的前n项和为Sn,且满足S15>0,S16<0,则当Sn最大时,n=( )
| A、6 | B、7 | C、8 | D、9 |
不等式x2-2x-3<0成立的一个必要不充分条件是( )
| A、-1<x<3 |
| B、0<x<3 |
| C、-2<x<3 |
| D、-2<x<1 |
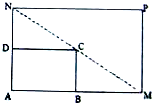 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知AB=3米,AD=2米.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知AB=3米,AD=2米.