题目内容
已知函数f(x)=
-(x-1)2+
,则函数f(x)的所有零点的和是( )
| 3 |
| |x-1|-2 |
| 3 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
考点:函数的零点
专题:计算题,作图题,函数的性质及应用
分析:令g(x)=
-x2+
;f(x)可看作g(x)向右平移1个单位得到,从而判断g(x)=
-x2+
是偶函数,且g(x)=
-x2+
一共有3个零点,从而求函数f(x)的所有零点的和.
| 3 |
| |x|-2 |
| 3 |
| 2 |
| 3 |
| |x|-2 |
| 3 |
| 2 |
| 3 |
| |x|-2 |
| 3 |
| 2 |
解答:
解:令g(x)=
-x2+
;
则易知g(x)=
-x2+
是偶函数,
又∵当x≥0时,
-x2+
=0的解得个数即
函数y=
与y=x2-
的交点个数,
作函数y=
与y=x2-
的图象如下,

有两个交点,且其中一个交点的横坐标为0;
故g(x)=
-x2+
一共有3个零点,
且3个零点之和为0;
而f(x)可看作g(x)向右平移1个单位得到,
故函数f(x)的所有零点的和是3×1=3;
故选C.
| 3 |
| |x|-2 |
| 3 |
| 2 |
则易知g(x)=
| 3 |
| |x|-2 |
| 3 |
| 2 |
又∵当x≥0时,
| 3 |
| |x|-2 |
| 3 |
| 2 |
函数y=
| 3 |
| x-2 |
| 3 |
| 2 |
作函数y=
| 3 |
| x-2 |
| 3 |
| 2 |

有两个交点,且其中一个交点的横坐标为0;
故g(x)=
| 3 |
| |x|-2 |
| 3 |
| 2 |
且3个零点之和为0;
而f(x)可看作g(x)向右平移1个单位得到,
故函数f(x)的所有零点的和是3×1=3;
故选C.
点评:本题考查了函数的零点的判断与应用,属于基础题.

练习册系列答案
相关题目
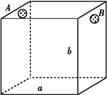 为处理含有某种杂质的污水,要制造一个底宽为2米的无盖长方体沉淀箱(如图),污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米,已知流出的水中该杂质的质量分数与a、b的乘积ab成反比,现有制箱材料60平方米,当a、b各为( )米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计)?
为处理含有某种杂质的污水,要制造一个底宽为2米的无盖长方体沉淀箱(如图),污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米,已知流出的水中该杂质的质量分数与a、b的乘积ab成反比,现有制箱材料60平方米,当a、b各为( )米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计)?| A、a=2,b=9 |
| B、a=9,b=2 |
| C、a=3,b=6 |
| D、a=6,b=3 |
设学生的考试成绩为G,则下面的代码的算法目的是( )


| A、计算50个学生的平均成绩 |
| B、计算50个学生中不及格的人数 |
| C、计算50个学生中及格的人数 |
| D、计算50个学生的总成绩 |
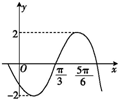 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图,则f(x)的表达式为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图象如图,则f(x)的表达式为( )A、f(x)=2sin(
| ||||
B、f(x)=2sin(x-
| ||||
C、f(x)=2sin(
| ||||
D、f(x)=2sin(2x-
|