题目内容
某幼儿园有教师30人,对他们进行年龄状况和受教育程度的调查,其结果如下:
(Ⅰ)从该幼儿园教师中随机抽取一人,求具有研究生学历的概率;
(Ⅱ)从幼儿园所有具有研究生学历的教师中随机抽取2人,求有35岁以下的研究生或50岁以上的研究生的概率.
| 本科 | 研究生 | 合计 | |
| 35岁以下 | 5 | 2 | 7 |
| 35~50岁(含35岁和50岁) | 17 | 3 | 20 |
| 50岁以上 | 2 | 1 | 3 |
(Ⅱ)从幼儿园所有具有研究生学历的教师中随机抽取2人,求有35岁以下的研究生或50岁以上的研究生的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(Ⅰ)根据概率公式计算即可
(Ⅱ)从这6人中任取2人,用列举法一一列举,共有15种等可能发生的基本事件.记“从幼儿园所有具有研究生学历的教师中随机抽取2人,有35岁以下的研究生或50岁以上的研究生”为事件B,则B中的结果共有15-3=12个,由此求得所求的事件的概率.
(Ⅱ)从这6人中任取2人,用列举法一一列举,共有15种等可能发生的基本事件.记“从幼儿园所有具有研究生学历的教师中随机抽取2人,有35岁以下的研究生或50岁以上的研究生”为事件B,则B中的结果共有15-3=12个,由此求得所求的事件的概率.
解答:
解:(Ⅰ)设:“从该幼儿园教师中随机抽取一人,具有研究生学历”为事件A
由题可知幼儿园总共有教师30人,其中“具有研究生学历”的共6人.
则P(A)=
=
儿园教师中随机抽取一人,具有研究生学历的概率为
.
(Ⅱ)设幼儿园中35岁以下具有研究生学历的教师用1,2表示,35~50岁(含35岁和50岁)具有研究生学历的教师为3,4,5,50岁以上具有研究生学历的教师为6,从幼儿园所有具有研究生学历的教师中随机抽取2人,所有可能结果有15个,它们是:12,13,14,15,16,23,24,25,26,34,35,36,45,46,56,共有15种抽法,
其中全是35~50岁(含35岁和50岁)的结果有3种,分别为:34,35,45,
记“从幼儿园所有具有研究生学历的教师中随机抽取2人,有35岁以下的研究生或50岁以上的研究生”为事件B,则B中的结果共有15-3=12个,
故所求概率为P(B)=
=
.
答:从幼儿园所有具有研究生学历的教师中随机抽取2人,有35岁以下的研究生或50岁以上的研究生的概率为
.
由题可知幼儿园总共有教师30人,其中“具有研究生学历”的共6人.
则P(A)=
| 6 |
| 30 |
| 1 |
| 5 |
儿园教师中随机抽取一人,具有研究生学历的概率为
| 1 |
| 5 |
(Ⅱ)设幼儿园中35岁以下具有研究生学历的教师用1,2表示,35~50岁(含35岁和50岁)具有研究生学历的教师为3,4,5,50岁以上具有研究生学历的教师为6,从幼儿园所有具有研究生学历的教师中随机抽取2人,所有可能结果有15个,它们是:12,13,14,15,16,23,24,25,26,34,35,36,45,46,56,共有15种抽法,
其中全是35~50岁(含35岁和50岁)的结果有3种,分别为:34,35,45,
记“从幼儿园所有具有研究生学历的教师中随机抽取2人,有35岁以下的研究生或50岁以上的研究生”为事件B,则B中的结果共有15-3=12个,
故所求概率为P(B)=
| 12 |
| 15 |
| 4 |
| 5 |
答:从幼儿园所有具有研究生学历的教师中随机抽取2人,有35岁以下的研究生或50岁以上的研究生的概率为
| 4 |
| 5 |
点评:本题考查古典概型及其概率计算公式,可以列举出试验发生包含的事件和满足条件的事件,应用列举法来解题是这一部分的最主要思想,属于基础题.

练习册系列答案
相关题目
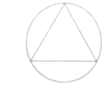 某人随机地向如图所示的正三角形及其外接圆区域内部设计(不包括三角形及其外接圆的边界),则针孔到正三角形内部(不包括边界)的概率为( )
某人随机地向如图所示的正三角形及其外接圆区域内部设计(不包括三角形及其外接圆的边界),则针孔到正三角形内部(不包括边界)的概率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
空间四边形ABCD中,若E、F、G、H分别为AB、BC、CD、DA边上的中点,则下列各式中成立的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
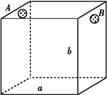 为处理含有某种杂质的污水,要制造一个底宽为2米的无盖长方体沉淀箱(如图),污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米,已知流出的水中该杂质的质量分数与a、b的乘积ab成反比,现有制箱材料60平方米,当a、b各为( )米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计)?
为处理含有某种杂质的污水,要制造一个底宽为2米的无盖长方体沉淀箱(如图),污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米,已知流出的水中该杂质的质量分数与a、b的乘积ab成反比,现有制箱材料60平方米,当a、b各为( )米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计)?| A、a=2,b=9 |
| B、a=9,b=2 |
| C、a=3,b=6 |
| D、a=6,b=3 |
设学生的考试成绩为G,则下面的代码的算法目的是( )


| A、计算50个学生的平均成绩 |
| B、计算50个学生中不及格的人数 |
| C、计算50个学生中及格的人数 |
| D、计算50个学生的总成绩 |