题目内容
5.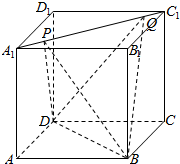 如图,已知棱长为1的正方体中ABCD-A1B1C1D1中,P,Q是面对角线A1C1上的两个不同动点,若PQ=1,则四面体BDPQ在该正方体六个面上的正投影的面积的和为2+2$\sqrt{2}$.
如图,已知棱长为1的正方体中ABCD-A1B1C1D1中,P,Q是面对角线A1C1上的两个不同动点,若PQ=1,则四面体BDPQ在该正方体六个面上的正投影的面积的和为2+2$\sqrt{2}$.
分析 分别判断四面体BDPQ在正方体六个面上的正投影的形状,进而求出四面体BDPQ在正方体六个面上的正投影的两种,相加可得答案.
解答  解:四面体BDPQ在上下两个底面上的投影是对角线互相垂直且对角线长度分别1和$\sqrt{2}$的四边形,其面积为定值$\frac{\sqrt{2}}{2}$,
解:四面体BDPQ在上下两个底面上的投影是对角线互相垂直且对角线长度分别1和$\sqrt{2}$的四边形,其面积为定值$\frac{\sqrt{2}}{2}$,
四面体BDPQ在四个侧面上的投影,均为上底为$\frac{\sqrt{2}}{2}$,下底和高均为1的梯形,其面积为定值$\frac{\sqrt{2}}{4}$$+\frac{1}{2}$,
故四面体BDPQ在该正方体六个面上的正投影的面积的和为定值2×$\frac{\sqrt{2}}{2}$+4×($\frac{\sqrt{2}}{4}$$+\frac{1}{2}$)=2+2$\sqrt{2}$,
故答案为:2+2$\sqrt{2}$.
点评 本题考查的知识点是平行投影,其中根据已知分析出四面体BDPQ在正方体六个面上的正投影的形状,是解答的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
4.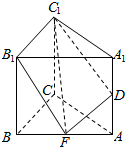 如图,已知直三棱柱ABC-A1B1C1的侧棱长是2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积是( )
如图,已知直三棱柱ABC-A1B1C1的侧棱长是2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积是( )
 如图,已知直三棱柱ABC-A1B1C1的侧棱长是2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积是( )
如图,已知直三棱柱ABC-A1B1C1的侧棱长是2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积是( )| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{2}{3}$ |