题目内容
10．若函数f（x）=$\frac{1}{x}$+2．则f（2x+1）=$\frac{1}{2x+1}$+2，x≠$-\frac{1}{2}$．分析 直接利用函数的解析式求解即可．
解答 解：f（x）=$\frac{1}{x}$+2．则f（2x+1）=$\frac{1}{2x+1}$+2，x≠$-\frac{1}{2}$．
故答案为：$\frac{1}{2x+1}$+2，x≠$-\frac{1}{2}$．
点评 本题考查函数的解析式的求法，考查计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
20．若不等式-2x2+bx+1＞0的解集$\{x|-\frac{1}{2}＜x＜m\}$，则b，m值是（ ）
| A． | 1，1 | B． | 1，-1 | C． | -1，1 | D． | -1，-1 |
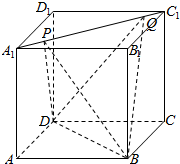如图，已知棱长为1的正方体中ABCD-A1B1C1D1中，P，Q是面对角线A1C1上的两个不同动点，若PQ=1，则四面体BDPQ在该正方体六个面上的正投影的面积的和为2+2$\sqrt{2}$．
2．若x＞0，y＞0，且x+y=$\frac{1}{3}$，则xy的最大值为（ ）
| A． | $\frac{2\sqrt{3}}{3}$ | B． | 2$\sqrt{3}$ | C． | $\frac{1}{9}$ | D． | $\frac{1}{36}$ |