题目内容
13.已知函数f(x)=cos($\frac{π}{3}$+x)•cos($\frac{π}{3}$-x),g(x)=$\frac{1}{2}$sin2x-$\frac{1}{4}$,函数h(x)=f(x)-g(x),则h(x)取得最大值时x的集合为{x|x=kπ-$\frac{π}{8}$,k∈Z}.分析 由三角函数公式化简可得h(x)=f(x)-g(x)=$\frac{\sqrt{2}}{2}$cos(2x+$\frac{π}{4}$),由三角函数的最值可得.
解答 解:由三角函数公式化简可得
f(x)=cos($\frac{π}{3}$+x)•cos($\frac{π}{3}$-x)
=($\frac{1}{2}$cosx-$\frac{\sqrt{3}}{2}$sinx)($\frac{1}{2}$cosx+$\frac{\sqrt{3}}{2}$sinx)
=$\frac{1}{4}$cos2x-$\frac{3}{4}$sin2x
=$\frac{1}{4}$•$\frac{1+cos2x}{2}$-$\frac{3}{4}$•$\frac{1-cos2x}{2}$
=$\frac{1}{2}$cos2x-$\frac{1}{4}$,
∴h(x)=f(x)-g(x)
=$\frac{1}{2}$cos2x-$\frac{1}{4}$-$\frac{1}{2}$sin2x+$\frac{1}{4}$
=$\frac{\sqrt{2}}{2}$cos(2x+$\frac{π}{4}$)
∴当2x+$\frac{π}{4}$=2kπ(k∈Z)时,h(x)取得最大值$\frac{\sqrt{2}}{2}$,
此时x的集合为{x|x=kπ-$\frac{π}{8}$,k∈Z}
故答案为:{x|x=kπ-$\frac{π}{8}$,k∈Z}
点评 本题考查三角函数恒等变换,涉及三角函数的最值,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知甲圆锥的半径是乙圆锥半径的3倍,它的高只有乙圆锥高的$\frac{1}{3}$,则甲圆锥与乙圆锥的体积之比为( )
| A. | 1:1 | B. | 3:1 | C. | 9:1 | D. | 1:9 |
2.若x>0,y>0,且x+y=$\frac{1}{3}$,则xy的最大值为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{36}$ |
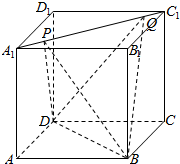 如图,已知棱长为1的正方体中ABCD-A1B1C1D1中,P,Q是面对角线A1C1上的两个不同动点,若PQ=1,则四面体BDPQ在该正方体六个面上的正投影的面积的和为2+2$\sqrt{2}$.
如图,已知棱长为1的正方体中ABCD-A1B1C1D1中,P,Q是面对角线A1C1上的两个不同动点,若PQ=1,则四面体BDPQ在该正方体六个面上的正投影的面积的和为2+2$\sqrt{2}$.