题目内容
17.已知函数f(x)=(a-1)x3+x2+(b-4)x+c为偶函数.则求函数g(x)=ax2+bx在区间[c,c+1]的值域.分析 根据函数f(x)为偶函数可得a,b的值,进而得到函数g(x)的解析式,结合二次函数的图象和性质,分类讨论,可得不同情况下函数的值域.
解答 解:∵函数f(x)=(a-1)x3+x2+(b-4)x+c为偶函数.
∴f(-x)=f(x),
即-(a-1)x3+x2-(b-4)x+c=(a-1)x3+x2+(b-4)x+c,
解得:a=1,b=4,
∴函数g(x)=x2+4x的图象是开口朝上,且以直线x=-2为对称轴的抛物线,
①若c+1<-2,即c<-3,则函数g(x)=x2+4x在区间[c,c+1]上为减函数,
当x=c时,函数取最大值c2+4c;当x=c+1时,函数取最小值c2+6c+5;
此时函数的值域为:[c2+6c+5,c2+4c],
②若$\frac{c+(c+1)}{2}$≤-2≤c+1,即-3≤c≤$-\frac{5}{2}$,则函数g(x)=x2+4x在区间[c,-2]上为减函数,在区间[-2,c+1]上为增函数,
当x=c时,函数取最大值c2+4c;当x=-2时,函数取最小值-4,
此时函数的值域为:[-4,c2+4c],
③若c≤-2<$\frac{c+(c+1)}{2}$,即$-\frac{5}{2}$<c≤-2,则函数g(x)=x2+4x在区间[c,-2]上为减函数,在区间[-2,c+1]上为增函数,
当x=c+1时,函数取最大值c2+6c+5;当x=-2时,函数取最小值-4,
此时函数的值域为:[-4,c2+6c+5],
④若c>-2,则函数g(x)=x2+4x在区间[c,c+1]上为增函数,
当x=c+1时,函数取最大值c2+6c+5;当x=c时,函数取最小值c2+4c;
此时函数的值域为:[c2+4c,c2+6c+5].
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

| A. | 1条或者3条 | B. | 1条或者2条 | C. | 2条或者3条 | D. | 4条或者3条 |
| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{36}$ |
| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
| A. | 30种 | B. | 65种 | C. | 35种 | D. | 70种 |
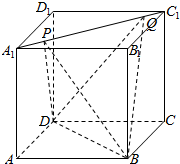 如图,已知棱长为1的正方体中ABCD-A1B1C1D1中,P,Q是面对角线A1C1上的两个不同动点,若PQ=1,则四面体BDPQ在该正方体六个面上的正投影的面积的和为2+2$\sqrt{2}$.
如图,已知棱长为1的正方体中ABCD-A1B1C1D1中,P,Q是面对角线A1C1上的两个不同动点,若PQ=1,则四面体BDPQ在该正方体六个面上的正投影的面积的和为2+2$\sqrt{2}$.