题目内容
20.求等差数列-2,1,4,7…的通项公式和前n项的和.分析 求出公差,利用等差数列通项公式以及求和公式求解即可.
解答 解:等差数列-2,1,4,7…的公差为:3;
通项公式an=-2+3(n-1)=3n-5
前n项的和:Sn=-2n+$\frac{n(n-1)}{2}×3$=$\frac{3}{2}{n}^{2}$-$\frac{7}{2}n$.
点评 本题考查等差数列通项公式以及前n项和的求法,考查计算能力.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
10.某几何体的三视图如图所示,则它的表面积为( )
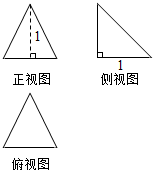

| A. | $\frac{{\sqrt{3}+\sqrt{7}+4}}{4}$ | B. | $\frac{{\sqrt{6}+2}}{2}$ | C. | $\frac{{\sqrt{2}+\sqrt{7}+1}}{2}$ | D. | $\frac{{\sqrt{2}+\sqrt{5}+1}}{2}$ |
11.下列说法中正确的是( )
| A. | “若$\overrightarrow a•\overrightarrow b=0$,则$\overrightarrow a⊥\overrightarrow b$”的否命题是“若$\overrightarrow a•\overrightarrow b≠0$,则$\overrightarrow a⊥\overrightarrow b$” | |
| B. | 命题“?x∈R,恒有x2+1>0”的否定是“?x0∈R,使得${x_0}^2+1<0$” | |
| C. | ?m∈R,使函数f(x)=x2+mx(x∈R)是奇函数 | |
| D. | 设p,q是简单命题,若p∧q是真命题,则(¬p)∨q也是真命题 |
12.已知圆C1:x2+y2-$\frac{2}{\sqrt{a}}$x+$\frac{1}{a}$-$\frac{9}{4}$=0,C2:x2+y2-$\frac{2}{\sqrt{b}}$y+$\frac{1}{b}$-$\frac{1}{4}$=0,其中a>0,b>0,a+b=1,则两圆公切线有多少条( )
| A. | 1条或者3条 | B. | 1条或者2条 | C. | 2条或者3条 | D. | 4条或者3条 |
9.在数列{an}中,若a1=$\frac{1}{2}$,an=$\frac{1}{1-{a}_{n-1}}$(n≥2,n∈N),则a2012的值为( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
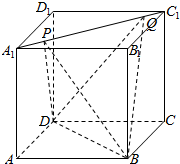 如图,已知棱长为1的正方体中ABCD-A1B1C1D1中,P,Q是面对角线A1C1上的两个不同动点,若PQ=1,则四面体BDPQ在该正方体六个面上的正投影的面积的和为2+2$\sqrt{2}$.
如图,已知棱长为1的正方体中ABCD-A1B1C1D1中,P,Q是面对角线A1C1上的两个不同动点,若PQ=1,则四面体BDPQ在该正方体六个面上的正投影的面积的和为2+2$\sqrt{2}$.