题目内容

4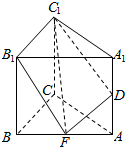．如图，已知直三棱柱ABC-A1B1C1的侧棱长是2，底面△ABC是等腰直角三角形，且∠ACB=90°，AC=2，E是AB的中点，D是AA1的中点，则三棱锥D-B1C1E的体积是（　　）
A．1B．$\frac{1}{3}$C．$\frac{\sqrt{2}}{3}$D．$\frac{2}{3}$

分析 求出底面DB1E的面积，求出C1到底面的距离，然后求解棱锥的体积．

解答 解：直三棱柱ABC-A1B1C1的侧棱长是2，底面△ABC是等腰直角三角形，且∠ACB=90°，
过C1作C1G⊥A1B1于G，则C1G⊥平面DB1E，C1G=$\sqrt{2}$．
三棱锥D-B1C1E的体积就是C1-DB1E的体积．
${S}_{{△DB}_{1}E}$=${S}_{{AA}_{1}{B}_{1}B}$-${S}_{{△B}_{1}BF}$-S△AED-${S}_{{△DA}_{1}{B}_{1}}$=$2×2\sqrt{2}$$-\frac{1}{2}×2×\sqrt{2}$$-\frac{1}{2}×\sqrt{2}×1$$-\frac{1}{2}×2\sqrt{2}×1$=$\frac{3\sqrt{2}}{2}$．
三棱锥D-B1C1E的体积是：$\frac{1}{3}×\frac{3\sqrt{2}}{2}×\sqrt{2}$=1．
故选：A．

点评 本题主要考查空间线面关系、几何体的体积等知识，考查学生分析解决问题的能力，属于中档题．

练习册系列答案
相关题目
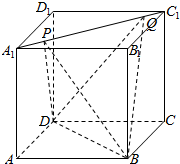5．如图，已知棱长为1的正方体中ABCD-A1B1C1D1中，P，Q是面对角线A1C1上的两个不同动点，若PQ=1，则四面体BDPQ在该正方体六个面上的正投影的面积的和为2+2$\sqrt{2}$．
6．求证：
（1）tan$\frac{α}{2}$=$\frac{sinα}{1+cosα}$=$\frac{1-cosα}{sinα}$；
（2）cosαsinβ=$\frac{1}{2}$[sin（α+β）-sin（α-β）]；
（3）sinα-sinβ=2cos$\frac{α-β}{2}$sin$\frac{α-β}{2}$．
3．设函数f（x）=$\left\{\begin{array}{l}{lo{g}_{4}（{x}^{2}+1），x≤0}\\{sinx，0＜x≤π}\end{array}\right.$，则不等式f（x）＞$\frac{1}{2}$的解集为（-∞，-1）∪（$\frac{π}{6}$，$\frac{5π}{6}$）．
10．已知A点坐标为（-1，0），B点坐标为（1，0），且动点M到A点的距离是4，线段MB的垂直平分线l交线段MA于点P．（1）求动点P的轨迹C方程；
（2）若P是曲线C上的点，求k=|PA|•|PB|的最大值和最小值．
9．函数f（x）=$\frac{ax+b}{{1+{x^2}}}$是定义在（-1，1）上的奇函数，且$f（\frac{1}{2}）=\frac{2}{5}$
（1）求f（x）的解析式；
（2）试判断f（x）在（-1，1）上的单调性，并利用函数单调性的定义证明；
（3）若f（t-1）+f（t）＜0，求实数t的取值范围．
16．五名男同学，三名女同学外出春游，平均分成两组，每组4人，则女同学不都在同一组的不同分法有（　　）
A．30种B．65种C．35种D．70种
13．已知双曲线与椭圆$\frac{x^2}{36}+\frac{y^2}{27}=1$有相同的焦点，且虚轴的长为4．
（Ⅰ）求双曲线的方程；
（Ⅱ）求双曲线的渐近线方程．
14．对于函数f1（x），f2（x），h（x），如果存在实数a，b使得h（x）=a•f1（x）+b•f2（x），那么称h（x）为f1（x），f2（x）的生成函数．
（1）函数f1（x）=x2-x，f2（x）=x2+x+1，h（x）=x2-x+1，h（x）是否为f1（x），f2（x）的生成函数？说明理由；
（2）设f1（x）=1-x，f2（x）=$\frac{{{x^2}-x+1}}{x-1}$，当a=b=1时生成函数h（x），求h（x）的对称中心（不必证明）；
（3）设f1（x）=x，${f_2}（x）=\frac{1}{x-1}$（x≥2），取a=2，b＞0，生成函数h（x），若函数h（x）的最小值是5，求实数b的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网