题目内容
14．如图，E，F分别是正方形ABCD的边BC，CD的中点，沿图中虚线折起来，它能形成怎样的几何体？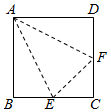
分析 根据图形折叠后B、C、D三点重合，得到直三棱锥，画出图形，说明结论即可．
解答 
解：由题意得，沿图中虚线折叠后，得到直三棱锥，
且三棱锥的底面为等腰直角△EFC，高为AC；
如图所示
点评 本题考查了平面图形折叠后所得到空间图形的应用问题，是基础题目．
练习册系列答案
相关题目
4．已知定义在R上的偶函数f（x），满足f（x+4）=f（x），f（x）=sinπx+2|sinπx|，x∈[0，2]，函数g（x）=f（x）-loga（x+$\frac{3}{2}$），若以g（x）=0在区间[-1，3]上至少6个根，则a的取值范围为（ ）
| A． | [${4}^{\frac{1}{3}}$，+∞） | B． | [${4}^{\frac{1}{3}}$，6] | C． | [4，+∞） | D． | [3，4] |
2．已知命题p；$\frac{1}{2}$≤x≤1，命题q：（x-a）（x-a-1）≤0，若￢p是￢q的必要不充分条件，则实数a的取值范围是（ ）
| A． | [0，$\frac{1}{2}$] | B． | [$\frac{1}{2}$，1] | C． | [$\frac{1}{3}$，$\frac{1}{2}$] | D． | $（\frac{1}{3}，\frac{1}{2}]$ |
9．不等式x2-2x+m＞0在R上恒成立的必要不充分条件是（ ）
| A． | m＞2 | B． | 0＜m＜1 | C． | m＞0 | D． | m＞1 |
（重点中学做）ABCD-A1B1C1D1是棱长为1的正方体，一个质点从A出发沿正方体的面对角线运动，每走完一条面对角线称为“走完一段”，质点的运动规则如下：运动第i段与第i+2所在直线必须是异面直线（其中i是正整数）．质点走完的第99段与第1段所在的直线所成的角是（ ）