题目内容
6.在函数y=xcosx,y=ex+x2,$y=lg\sqrt{{x^2}-2}$,y=xsinx偶函数的个数是( )| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 根据函数奇偶性的定义分别进行判断即可.
解答 解:①f(-x)=-xcos(-x)=-xcosx=-f(x),则y=xcosx是奇函数,不满足条件.
②当x=1时,f(1)=e+1,当x=-1时,f(-1)=$\frac{1}{e}$+1≠f(1),则y=ex+x2,不是偶函数,不满足条件.
③由x2-2>0得x>$\sqrt{2}$或x<-$\sqrt{2}$,
此时f(-x)=lg$\sqrt{(-x)^{2}-2}$=lg$\sqrt{{x}^{2}-2}$,则y=lg$\sqrt{{x}^{2}-2}$,是偶函数,
④f(-x)=-xsin(-x)=xsinx=f(x),则y=xsinx是偶函数,满足条件.
故偶函数的个数为2个,
故选:B.
点评 本题主要考查函数奇偶性的判断,根据函数奇偶性的定义是解决本题的关键.比较基础.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
16.焦点是F(0,1)的抛物线的标准方程是( )
| A. | x2=4y | B. | y2=4x | C. | x2=-4y | D. | y2=-4x |
17.在集合{x|x=$\frac{nπ}{6}$,n=1,2,3…,10}中任取一个元素,所取元素恰好满足方程sinx=$\frac{\sqrt{3}}{2}$的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
1.已知x,y满足不等式$\left\{\begin{array}{l}x-4y≤-3\\ 3x+5y≤25\\ x≥1\end{array}\right.$,则函数z=2x+y取得最大值是( )
| A. | 3 | B. | $\frac{13}{2}$ | C. | 12 | D. | 23 |
11.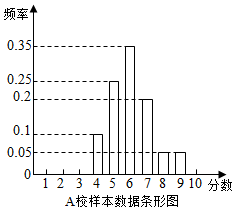 某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
B校样本数据统计表:
(Ⅰ)计算两校样本数据的均值和方差,并根据所得数据进行比较.
(Ⅱ)从A校样本数据成绩分别为7分、8分和9分的学生中按分层抽样方法抽取6人,若从抽取的6人中任选2人参加更高一级的比赛,求这2人成绩之和大于或等于15的概率.
 某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:
某市组织高一全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如表:B校样本数据统计表:
| 成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数(个) | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
(Ⅱ)从A校样本数据成绩分别为7分、8分和9分的学生中按分层抽样方法抽取6人,若从抽取的6人中任选2人参加更高一级的比赛,求这2人成绩之和大于或等于15的概率.
18.已知在某个回归分析中有甲、乙、丙三个模型,其R2的值依次为0.64、0.80和0.98,则下列说法正确的是( )
| A. | 甲模型拟合效果最好 | B. | 乙模型拟合效果最好 | ||
| C. | 丙模型拟合效果最好 | D. | 拟合效果与R2的值无关 |