题目内容
6.已知长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2.(1)求A1到平面AB1D距离;
(2)求D到平面A1BD1距离.
分析 (1)根据V${\;}_{{A}_{1}-A{B}_{1}D}$=V${\;}_{D-{A}_{1}A{B}_{1}}$列方程求出;
(2)根据V${\;}_{B-{A}_{1}{D}_{1}D}$=V${\;}_{D-{A}_{1}B{D}_{1}}$列方程求出.
解答 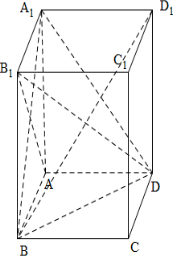 解:(1)∵长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,
解:(1)∵长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,
∴AB1=$\sqrt{4+1}$=$\sqrt{5}$,
∴S${\;}_{△A{B}_{1}D}$=$\frac{1}{2}×AD×A{B}_{1}$=$\frac{1}{2}×1×\sqrt{5}$=$\frac{\sqrt{5}}{2}$,
V${\;}_{{A}_{1}-A{B}_{1}D}$=V${\;}_{D-{A}_{1}A{B}_{1}}$=$\frac{1}{3}{S}_{△{A}_{1}A{B}_{1}}•AD$=$\frac{1}{3}×\frac{1}{2}×1×2×1$=$\frac{1}{3}$,
设A1到平面AB1D距离为h,则V${\;}_{{A}_{1}-A{B}_{1}D}$=$\frac{1}{3}$S${\;}_{△A{B}_{1}D}$•h,
即$\frac{1}{3}$=$\frac{1}{3}×\frac{\sqrt{5}}{2}×h$,
∴h=$\frac{2\sqrt{5}}{5}$.
∴A1到平面AB1D距离为$\frac{2\sqrt{5}}{5}$.
(2)设D到平面A1BD1距离为h2,
∵V${\;}_{B-{A}_{1}{D}_{1}D}$=V${\;}_{D-{A}_{1}B{D}_{1}}$,即$\frac{1}{3}{S}_{△{A}_{1}{D}_{1}D}•AB$=$\frac{1}{3}{S}_{△{A}_{1}B{D}_{1}}•{h}_{2}$,
∴$\frac{1}{3}×\frac{1}{2}×1×2×1$=$\frac{1}{3}×\frac{1}{2}×1×\sqrt{5}$×h2,
∴h2=$\frac{2\sqrt{5}}{5}$.
∴D到平面A1BD1距离为$\frac{2\sqrt{5}}{5}$.
点评 本题考查了点面距离的计算,可用等积法、向量法、或定义法求出,属于中档题.

 备战中考寒假系列答案
备战中考寒假系列答案| A. | y=±x | B. | $y=±\sqrt{2}x$ | C. | $y=±\sqrt{3}x$ | D. | y=±2x |
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
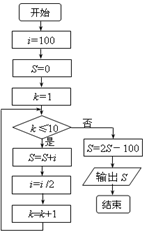 一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( )
一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( )| A. | 小球第10次着地时向下的运动共经过的路程 | |
| B. | 小球第11次着地时向下的运动共经过的路程 | |
| C. | 小球第10次着地时一共经过的路程 | |
| D. | 小球第11次着地时一共经过的路程 |
| A. | $\frac{π}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
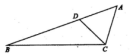 如图,在△ABC中,D为线段AB上的点,且AB=3AD,AC=AD,CB=3CD,则$\frac{sin2B}{sinA}$=$\frac{7}{9}$.
如图,在△ABC中,D为线段AB上的点,且AB=3AD,AC=AD,CB=3CD,则$\frac{sin2B}{sinA}$=$\frac{7}{9}$.