题目内容
 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:由图象可得A=2,由周期公式可得ω=2,代入点(
,2)解三角方程可得φ值,可得解析式.
| 5π |
| 12 |
解答:
解:由图象可得A=2,周期T=
=2(
-
),解得ω=2,
∴y=2sin(2x+φ),由图象过点(
,2),
∴2sin(
+φ)=2,解得
+φ=2kπ+
,k∈Z,
解得φ=2kπ-
,∵|φ|<
,∴φ=-
∴所求函数解析式为:y=2sin(2x-
)
故答案为:y=2sin(2x-
).
| 2π |
| ω |
| 11π |
| 12 |
| 5π |
| 12 |
∴y=2sin(2x+φ),由图象过点(
| 5π |
| 12 |
∴2sin(
| 5π |
| 6 |
| 5π |
| 6 |
| π |
| 2 |
解得φ=2kπ-
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
∴所求函数解析式为:y=2sin(2x-
| π |
| 3 |
故答案为:y=2sin(2x-
| π |
| 3 |
点评:本题考查三角函数解析式的求解,涉及系数的意义,属基础题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知抛物线y=ax2-2x+1与x轴没有交点,那么该抛物线的顶点所在的象限是( )
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |
在△ABC中,A、B、C所对的边长分别是a、b、c,其中a=2,b=2,C=60°,则△ABC的面积为( )
| A、1 | ||
| B、2 | ||
C、3
| ||
D、
|
若函数f(x)=Asin2ωx(A>0,ω>0)在x=1处取得最大值,则f(x+1)的奇偶性为( )
| A、偶函数 |
| B、奇函数 |
| C、既是奇函数又是偶函数 |
| D、非奇非偶函数 |
为了得到函数f(x)=cos(2x+
)的图象,只要把函数g(x)=
f′(x)的图象( )
| π |
| 4 |
| 1 |
| 2 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
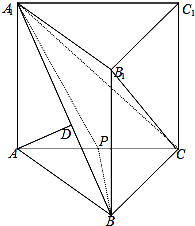 如图,直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.P为AC的中点.
如图,直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.P为AC的中点.