题目内容
3.设函数f(x)=$\left\{\begin{array}{l}{lo{g}_{4}({x}^{2}+1),x≤0}\\{sinx,0<x≤π}\end{array}\right.$,则不等式f(x)>$\frac{1}{2}$的解集为(-∞,-1)∪($\frac{π}{6}$,$\frac{5π}{6}$).分析 根据已知分段函数的解析式,分类讨论满足f(x)>$\frac{1}{2}$的x,最后综合讨论结果,可得答案.
解答 解:当x≤0时,解f(x)=$lo{g}_{4}({x}^{2}+1)$>$\frac{1}{2}$得:x<-1,或x>1(舍去),
当0<x<π时,解f(x)=sinx>$\frac{1}{2}$得:$\frac{π}{6}$<x<$\frac{5π}{6}$,
综上所述,不等式f(x)>$\frac{1}{2}$的解集为(-∞,-1)∪($\frac{π}{6}$,$\frac{5π}{6}$),
故答案为:(-∞,-1)∪($\frac{π}{6}$,$\frac{5π}{6}$)
点评 本题考查的知识点是分段函数的应用,对数不等式和三角不等式的解法,难度中档.

练习册系列答案
相关题目
18.已知函数f(x)=cosωx(sinωx+$\sqrt{3}$cosωx)(ω>0),如果存在实数x0,使得对任意的实数x,都有f(x0)≤f(x)≤f(x0+2016π)成立,则ω的最小值为( )
| A. | $\frac{1}{2016π}$ | B. | $\frac{1}{4032π}$ | C. | $\frac{1}{2016}$ | D. | $\frac{1}{4032}$ |
4.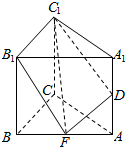 如图,已知直三棱柱ABC-A1B1C1的侧棱长是2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积是( )
如图,已知直三棱柱ABC-A1B1C1的侧棱长是2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积是( )
 如图,已知直三棱柱ABC-A1B1C1的侧棱长是2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积是( )
如图,已知直三棱柱ABC-A1B1C1的侧棱长是2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积是( )| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{2}{3}$ |
2.曲线C:$\frac{x^2}{4-k}+\frac{y^2}{k-1}$=1表示双曲线,则k的取值范围为( )
| A. | 1<k<4 | B. | k>4 | C. | k<0 | D. | k<1或k>4 |