题目内容
甲和乙两人约定凌晨在九龙广场喷水池旁见面,约定谁先到后必须等10分钟,这时若另一人还没有来就可以离开.假设甲在0点到1点内到达,且何时到达是等可能的,
(1)如果乙是0:40分到达,求他们能会面的概率;
(2)如果乙在0点到1点内到达,且何时到达是等可能的,求他们能会面的概率.
(1)如果乙是0:40分到达,求他们能会面的概率;
(2)如果乙在0点到1点内到达,且何时到达是等可能的,求他们能会面的概率.
考点:几何概型
专题:概率与统计
分析:(1)由题意知本题是一个几何概型,试验发生包含的所有事件对应的集合是Ω={x|0<x<60}做出集合对应的线段,写出满足条件的事件对应的集合和线段,根据长度之比得到概率.
(2)从0点开始计时,设甲经过x分钟到达,乙经过y分钟到达,可得x、y满足的不等式线组对应的平面区域为如图的正方形OABC,而甲乙能够见面,x、y满足的平面区域是图中的六边形OEFBGH.分别算出图中正方形和六边形的面积,相除即可得到两人能见面的概率.
(2)从0点开始计时,设甲经过x分钟到达,乙经过y分钟到达,可得x、y满足的不等式线组对应的平面区域为如图的正方形OABC,而甲乙能够见面,x、y满足的平面区域是图中的六边形OEFBGH.分别算出图中正方形和六边形的面积,相除即可得到两人能见面的概率.
解答:
解:(1)由题意知本题是一个几何概型,
∵试验发生包含的所有事件对应的集合是Ω={x|0<x<60}
集合对应的面积是长为60的线段,
而满足条件的事件对应的集合是A═{x|30<x<50}
得到 其长度为20
∴两人能够会面的概率是
=
;
(2)由题意知本题是一个几何概型,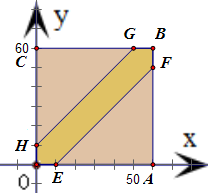 该不等式对应的平面区域是图中的六边形OEFBGH
该不等式对应的平面区域是图中的六边形OEFBGH
∵S正方形OABC=60×60=3600,
S六边形OEFBGH=S正方形OABC-2S△AEF=1100
因此,甲乙能见面的概率P=
=
∵试验发生包含的所有事件对应的集合是Ω={x|0<x<60}
集合对应的面积是长为60的线段,
而满足条件的事件对应的集合是A═{x|30<x<50}
得到 其长度为20
∴两人能够会面的概率是
| 20 |
| 60 |
| 1 |
| 3 |
(2)由题意知本题是一个几何概型,
 该不等式对应的平面区域是图中的六边形OEFBGH
该不等式对应的平面区域是图中的六边形OEFBGH∵S正方形OABC=60×60=3600,
S六边形OEFBGH=S正方形OABC-2S△AEF=1100
因此,甲乙能见面的概率P=
| S正方形OABC |
| S六边形OEFBGH |
| 11 |
| 36 |
点评:本题的难点是把时间分别用x,y坐标来表示,从而把时间长度这样的一维问题转化为平面图形的二维面积问题,转化成面积型的几何概型问题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
定义在R上的偶函数,f(x)满足:对任意的x1,x2∈(-∞,0](x1≠x2),有(x1-x2)[f(x2)-f(x1)]>0,则当n∈N*时,有( )
| A、f(-n)<f(n-1)<f(n+1) |
| B、f(n-1)<f(-n)<f(n+1) |
| C、f(n+1)<f(-n)<f(n-1) |
| D、f(n+1)<f(n-1)<f(-n) |
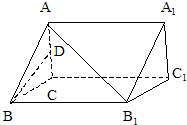 在空间平移正△ABC到△A1B1C1得到如图所示的几何体,若D是AC的中点,AA1⊥平面ABC,AA1:AB=
在空间平移正△ABC到△A1B1C1得到如图所示的几何体,若D是AC的中点,AA1⊥平面ABC,AA1:AB=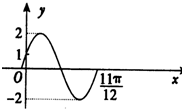 已知函数f(x)=A sin(ωx+ϕ)(A>0,ω>0,|φ|<
已知函数f(x)=A sin(ωx+ϕ)(A>0,ω>0,|φ|<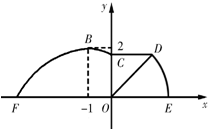 如图,某市准备在道路EF的一侧修建一条运动比赛道,赛道的前一部分为曲线段FBC.该曲线段是函数y=Asin(ωx+
如图,某市准备在道路EF的一侧修建一条运动比赛道,赛道的前一部分为曲线段FBC.该曲线段是函数y=Asin(ωx+