题目内容
14.已知函数f(x)=ex-1,g(x)=ln(x+1),直线l与y=f(x)的图象相切,与y=g(x)的图象也相切,则直线的l方程是y=x.分析 由已知函数解析式画出图象,可得两函数有唯一交点O(0,0),求出两函数在O(0,0)处的切线都是y=x,则答案可求.
解答 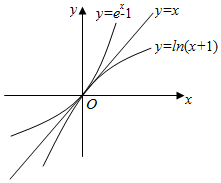 解:f(x)=ex-1与g(x)=ln(x+1)互为反函数,其图象如图,
解:f(x)=ex-1与g(x)=ln(x+1)互为反函数,其图象如图,
其公共点为O(0,0),
由f(x)=ex-1,得f′(x)=ex,
∴f′(0)=1,
曲线f(x)=ex-1在O(0,0)处的切线方程为y=x,
由g(x)=ln(x+1),得g′(x)=$\frac{1}{x+1}$,
∴g′(0)=1,
曲线g(x)=ln(x+1)在O(0,0)处的切线方程为y=x,
∴曲线f(x)=ex-1与曲线g(x)=ln(x+1)的公切线为y=x.
故答案为:y=x.
点评 本题考查利用导数研究过曲线上某点处的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处的导数值,是中档题.

练习册系列答案
相关题目
4.i是虚数单位,(i+1)(i+2)=( )
| A. | 1+3i | B. | 1-3i | C. | -1+3i | D. | -1-3i |
5.以下结论正确的是( )
| A. | 若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点 | |
| B. | 函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点 | |
| C. | 若函数y=f(x)在x0处取得极值,且f′(x0)存在,则必有f′(x0)=0 | |
| D. | 若函数y=f(x)在x0处连续,则f′(x0)一定存在 |
6.在△ABC中,已知a、b、c分别表示∠A、∠B、∠C所对边的长,若$(a+b+c)(c+b-a)=(2-\sqrt{3})bc$,则∠A=( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
 如图所示,以向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$为边作?AOBD,又$\overrightarrow{BM}$=$\frac{1}{3}$$\overrightarrow{BC}$,$\overrightarrow{CN}$=$\frac{1}{3}$$\overrightarrow{CD}$,用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{OM}$、$\overrightarrow{ON}$、$\overrightarrow{MN}$.
如图所示,以向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$为边作?AOBD,又$\overrightarrow{BM}$=$\frac{1}{3}$$\overrightarrow{BC}$,$\overrightarrow{CN}$=$\frac{1}{3}$$\overrightarrow{CD}$,用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{OM}$、$\overrightarrow{ON}$、$\overrightarrow{MN}$.