题目内容
已知函数f(x)=x2-2x,集合M={(x,y)|f(x)+f(y)≤2},集合N={(x,y)|f(x)≤f(y)},则集合M∩N的元素构成的图形的面积是 .
考点:简单线性规划,交集及其运算,二次函数的性质
专题:不等式的解法及应用
分析:根据条件确定结合M,N对应的图象,利用数形结合即可得到结论.
解答:
 解:由f(x)+f(y)≤2得x2-2x+y2-2y≤2,
解:由f(x)+f(y)≤2得x2-2x+y2-2y≤2,
即(x-1)2+(y-1)2≤4,即结合M为半径为2的圆及其内部,
由f(x)≤f(y)得x2-2x≤y2-2y,
即(x-y)(x+y-2)≤0,
作出集合M,N对应的图象如图:
则集合M∩N的元素构成的图形为阴影部分,对应的面积为圆面积的
,
即
×π×22=2π.
故答案为:2π
 解:由f(x)+f(y)≤2得x2-2x+y2-2y≤2,
解:由f(x)+f(y)≤2得x2-2x+y2-2y≤2,即(x-1)2+(y-1)2≤4,即结合M为半径为2的圆及其内部,
由f(x)≤f(y)得x2-2x≤y2-2y,
即(x-y)(x+y-2)≤0,
作出集合M,N对应的图象如图:
则集合M∩N的元素构成的图形为阴影部分,对应的面积为圆面积的
| 1 |
| 2 |
即
| 1 |
| 2 |
故答案为:2π
点评:本题主要考查二元一次不等式组表示平面区域,以及区域面积的计算,利用数形结合是解决本题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
从1,2,3,…,20这20个正整数中,每次取3个不同的数组成等比数列,则不同等比数列的个数共有( )
| A、10 | B、16 | C、20 | D、22 |
已知双曲线
-
=1(a>0,b>0),过双曲线的一个焦点作实轴的垂线交双曲线于A、B两点,若
•
=0(O为坐标原点),则双曲线的离心率e等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| OA |
| OB |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案,在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%,则下列哪个奖励模型比较符合该公司的要求( )
| A、y=0.25x | |||
| B、y=log7x+1 | |||
| C、y=1.002x | |||
D、y=
|
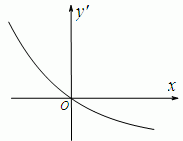 已知函数y=f(x)的导函数f′(x)的图象大致为如图,且f(15)=
已知函数y=f(x)的导函数f′(x)的图象大致为如图,且f(15)=