题目内容
若抛物线y2=2px(p>0)的准线经过双曲线x2-y2=1的左顶点,则p= .
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先求出x2-y2=1的左顶点,得到抛物线y2=2px的准线,依据p的意义求出它的值.
解答:
解:双曲线x2-y2=1的左顶点为(-1,0),
故抛物线y2=2px的准线为x=-1,
∴
=1,∴p=2,
故答案为:2.
故抛物线y2=2px的准线为x=-1,
∴
| p |
| 2 |
故答案为:2.
点评:本题考查抛物线和双曲线的简单性质,以及抛物线方程 y2=2px中p的意义.

练习册系列答案
相关题目
点F是双曲线y2-
=1的焦点,过F的直线l与双曲线同一支交于两点,则直线l的倾斜角的取值范围是( )
| x2 |
| 3 |
A、[
| ||||
B、(
| ||||
C、[
| ||||
D、(0,
|
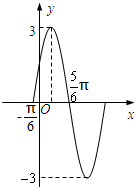 如图f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
如图f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<